22

Bug introduced in 11.1

Take the simple path defined by a line through a set of points 

pts = {{0, 0}, {0, 1.5}, {0.05, 1.5}, {0.05, 0.5}, {0.1, 0.5}, {0.1,  1.5},
{0.15, 1.5}, {0.15, 0.5}, {0.2, 0.5}, {0.2, 1.5}, {0.25, 1.5}, {0.25, 0.5},
{0.3, 0.5}, {0.3, 1.5}, {0.35, 1.5}, {0.35, 0}}

reg = Line[pts];

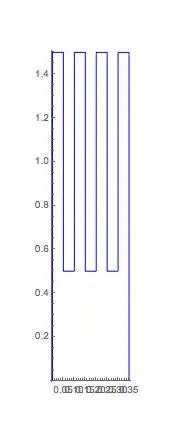
This can be visualized using Graphics

Graphics[{Blue, reg}, Axes -> True]

image

Both RegionMeasure and ArcLength should give us the length of the line and in fact it does give us a number 

RegionMeasure@reg
(* 7.85 *)
ArcLength@reg
(* 7.85 *)

This is wrong however!

This gives the sequence of the individual arc lengths:

FoldPairList[{Abs@Total[#2 - #1], #2} &, {0, 0}, pts]
(* {0., 1.5, 0.05, 1., 0.05, 1., 0.05, 1., 0.05, 1., 0.05, 1., 0.05, 1., 0.05, 1.5} *)

The sum of this sequence is $9.35$ not $7.85$.

Sanity check: Count the line segments on screen. There are two segments of length $1.5$, seven segments of length $0.05$, and six segments of length $1$. So in total: $2\times1.5 + 7\times0.05 + 6\times1 = 9.35$

I use Mathematica 11.1.1.0 on Mac OS 10.12.6

Edit in response to comments:

When I copy and paste pts from SE I also get $9.35$. Try the following which I used to generate pts in the first place:

pts2 = AnglePath[{{1.5, 90.°}, {0.05, -90.°}, {1, -90.°}, {0.05, 90.°}, {1, 90.°},
{0.05, -90.°}, {1, -90.°},{0.05, 90.°}, {1, 90.°}, {0.05, -90.°}, {1, -90.°},
{0.05, 90.°}, {1, 90.°}, {0.05, -90.°}, {1.5, -90.°}}] //Chop

and check that pts and pts2 are in fact equal

pts == pts2
(* True *)

Now try RegionMeasure@Line@pts2. For me this gives $7.85$. Seems the culprit is AnglePath.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Sascha
  • 8,459
  • 2
  • 32
  • 66
  • When you suspect a bug, always tell us the version. In 11.1.1 I get 9.35. – Szabolcs Aug 08 '17 at 07:43
  • I entered the commands from your post in the same order as you showed them, and got 9.35 with M11.1.1 on OS X 10.12.6 as well. – Szabolcs Aug 08 '17 at 07:47
  • 1
    Correct answers on 10.3 win – ciao Aug 08 '17 at 07:48
  • @Szabolcs See me edit. – Sascha Aug 08 '17 at 08:02
  • Yes, I can reproduce it. Neither of those lists, or their sublists, are packed, so that is not what is causing them to be different. – Szabolcs Aug 08 '17 at 08:06
  • It has to do with the specific numerical values somehow. For example, diff = pts-pts2, then ArcLength@Line[pts] is correct and ArcLength@Line[pts + diff] is not, even though Chop[diff] is all zeros. – Szabolcs Aug 08 '17 at 08:07
  • 2
    In 10.4 under Linux - everything ok; however, in 11.1 (under Linux) RegionMeasure@Line@pts2 gives indeed 7.85. ArcLength@Line[Chop[pts + diff]] gives 7.85 (in 11.1) but ArcLength@Line[pts + Chop@diff] gives 9.35; diff are not exactly zeros, but are off by 10^-16. There are no problems with the diff approach in v10.4, however. Another bug in version 11 - that's why I'm still using v10.4. – corey979 Aug 08 '17 at 08:20
  • Can you report this to Wolfram please? 11.0.1 does not have the problem. – Szabolcs Aug 08 '17 at 09:03
  • @Szabolcs I reported this to Wolfram with a link to this discussion. – Sascha Aug 08 '17 at 09:12
  • 2
    The problem indeed lies with the processing of polylines. ArcLength[RegionUnion[Line /@ Partition[pts, 2, 1]]] gives the correct answer on 11.1. – J. M.'s missing motivation Aug 08 '17 at 14:21
  • 2
    Filed a bug report, thanks for the example. The difference between pts and pts2 is because only 6 digits are printed by default, see InputForm[pts2]. – ilian Aug 08 '17 at 14:58

1 Answers1

13

The problem seems to arise from a bug in Region`DisjointSegments, which drops segments. I don't understand how it works, but I thought it probably has to do with rounding error and might depend on the precision of the points. Also, translating the coordinates away from 0 should help, which it does. It interesting that the distance translated the points affects discontinuously which segments are dropped. Perhaps the most disturbing occurrence is the rare result shown below: 

Manipulate[
 With[{p = SetPrecision[t + pts2, ReleaseHold@prec]},
  foo = Select[Region`DisjointSegments[Line[p]],
    Min[Abs@Differences@#, Infinity] > 10^-8 &];
  If[Length@foo != 0, Print[t -> foo]];
  Graphics[
   {Line[p],
    Red, Thickness[0.02], Line@Region`DisjointSegments[Line[p]]},
   PlotRange -> {{t - 0.02, t + 0.4}, {t - 0.05, t + 1.55}}, 
   AspectRatio -> 1,
   PlotLabel -> {t, RegionMeasure@Line[p]}
   ]],
 {{t, -0.09999999999999998`}, -0.6, 0.5, Appearance -> "Labeled"},
 {prec, {MachinePrecision, HoldForm@$MachinePrecision, HoldForm[$MachinePrecision + 1]}}
 ]

Mathematica graphics

It turns out that Region`DisjointSegments promotes MachinePrecision coordinates to the arbitrary precision $MachinePrecision. Setting prec to $MachinePrecision seems to have no effect. Bumping it up by 1 more seems to fix the bug. (In V11.0, promotion to $MachinePrecision was also used, so it is not the change that introduced the bug.)

Michael E2
  • 235,386
  • 17
  • 334
  • 747