I have checked all issues regarding to solving nonlinear PDE numerically. I however try to solve following equation via NDSolve function and get some troubles.
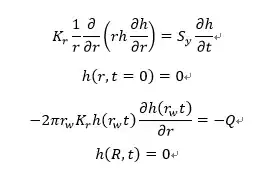
And this is my code for above-mentioned equations
rw = 0.05;
Sy = 0.15;
Kr = 0.0001*3600;
Q = 0.01;
sys = {Sy*Derivative[0, 1][h][r, t] ==
Kr*h[r, t]*((Derivative[2, 0][h][r, t] + Derivative[1, 0][h][r, t]/
r) + (Derivative[1, 0][h][r, t])^2),
2*Pi*rw*Kr*h[rw, t]*Derivative[1, 0][h][rw, t] == -Q,
h[100, t] == 0,
h[r, 0] == 0.00001
}; sol =
NDSolve[sys, {h}, {r, rw, 100}, {t, 0, 100000},
Method -> "MethodOfLines"]
But the value evaluated by the numerical result is equal to it's initial condition and obviously wrong. Do I miss something in the code?
h[100, t] == 0, h[r, 0] == 0.00001tries to assign two different values toh[100, 0]. This needs to be fixed. Also,2*Pi*rw*Kr*h[rw, t]*Derivative[1, 0][h][rw, t] == -Qis an unusual boundary condition, and I am uncertain howNDSolvewill respond to it. – bbgodfrey Aug 10 '17 at 23:45Method -> {"MethodOfLines", "DifferentiateBoundaryConditions" -> {True, "ScaleFactor" -> 100}}toNDSolvewill fix your code. (You'll probably needPlotRange->AllinPlot3D, too. ) – xzczd Sep 16 '17 at 14:34