1$\sigma$ contour plot for a two-dimensional Gaussian

Question

Say I have a 2D Gaussian with $$\mu=(\mu_1,\mu_2)$$ and $$ \Sigma= \left( {\begin{array}{cc} \sigma_{11}^2 & \rho \sigma_{11} \sigma_{22} \\ \rho \sigma_{11} \sigma_{22} & \sigma_{22}^2 \\ \end{array} } \right) $$

For example

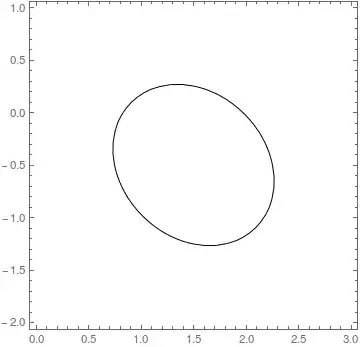
p = {m1 -> 1.5, m2 -> -0.5, s11 -> 0.5, s22 -> 0.5, r -> -0.2};

ContourPlot[
 PDF[MultinormalDistribution[{m1, m2}, {{s11^2, r s11 s22}, {r s11 s22, s22^2}}] /. p, {x, y}],
  {x, 0, 3.}, {y, -2, 1},
 Contours -> {0.2}, ContourShading -> None]

[Contours -> {0.2} inserted only for illustration, just to have any number to make a plot.]

---

How can I plot the 1$\sigma$ contour of the 2D Gaussian? It encompasses $\approx 0.39$ of the volume under the surface (being analogous to the 0.68 fraction marking the 1$\sigma$ region in the 1D Gaussian case).

So, the precise questions are (a) at what height of the PDF should I place the 1$\sigma$ contour? (Note: I can extract the maximum max of the PDF and easily plot, e.g., the contour corresponding to FWHM with Contours -> {1/2 max}.) And, if it's not that straightforward, my next idea would be (b) to to find the proper value via numerical integration (how to set this up?).

Answer 1

I don't know what a "$1\sigma$ contour of the 2D Gaussian" is but if you want a specific volume (between 0 and 1), then the following will get you the contour height for the bivariate normal:

p = {m1 -> 1.5, m2 -> -0.5, s11 -> 0.5, s22 -> 0.5, r -> -0.2};

(* Contour of interest *)
α = 0.39  (* Desired volume *)
c = Exp[-InverseCDF[ChiSquareDistribution[2], α]/2]/(2 π s11 s22 (1 - r^2)) /. p

ContourPlot[PDF[MultinormalDistribution[{m1, m2}, {{s11^2, r s11 s22}, {r s11 s22, s22^2}}] /. p, {x, y}],
 {x, 0, 3.}, {y, -2, 1}, Contours -> {c}, ContourShading -> None]

(* As a check:  Do the integration... *)
pdf = PDF[MultinormalDistribution[{m1, m2}, {{s11^2, r s11 s22}, {r s11 s22, s22^2}}], {x, y}] /. p;
xmin = m1 - 10 s11 /. p;
xmax = m1 + 10 s11 /. p;
ymin = m2 - 10 s22 /. p;
ymax = m2 + 10 s22 /. p;
NIntegrate[pdf Boole[((x - m1)^2/s11^2 + (y - m2)^2/s22^2 - 2 r (x - m1) (y - m2)/(s11 s22))/(1 - r^2) <= 
 InverseCDF[ChiSquareDistribution[2], α] /. p], {x, xmin, xmax}, {y, ymin, ymax}]
(* 0.39 *)