How to plot a color consistently in Plot3D with 2D projection curve?

Question

I use this code to draw three-dimensional surfaces and show the curves at the bottom. But does not give me the result required:

u[x_, y_] := x + y - x y
contour = 
  ContourPlot[u[x, y], {x, 0, 1}, {y, 0, 1}, PlotRange -> {0, 1}, 
   Axes -> False, Contours -> 15, PlotPoints -> 50, 
   PlotRangePadding -> 0, 
   ContourShading -> {{Opacity[.3], Blue}, {Opacity[.8], LightBlue}}];
potential1 = 
  Plot3D[u[x, y], {x, 0, 1}, {y, 0, 1}, PlotRange -> {0, 1}, 
   ClippingStyle -> None, MeshFunctions -> {#3 &}, Mesh -> 15, 
   MeshStyle -> Opacity[.5], 
   MeshShading -> {{Opacity[.3], Blue}, {Opacity[.8], LightBlue}}, 
   PlotRange -> {Automatic, Automatic, {min, 2}}, 
   Lighting -> "Neutral"];
Show[potential1, 
 Graphics3D[contour[[1]] /. {x_Real, y_Real} :> {x, y, 0}], 
 BoxRatios -> {1, 1, 0.6}, FaceGrids -> {Back, Left}]

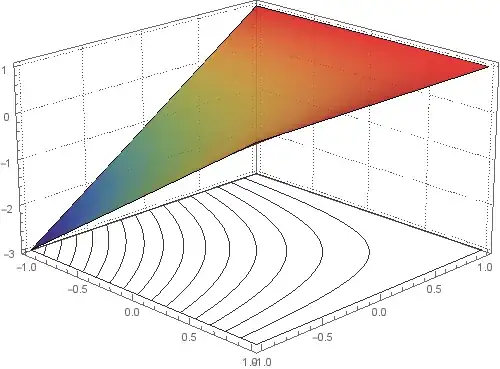
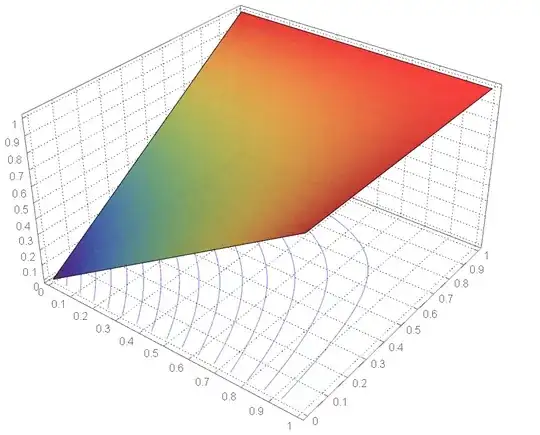
I need to have a three-dimensional drawing (Plot3D) that shows curves only better as in the following figures:

Is there a similar result to this plotting as in the pictures?

Or it's in other programs?

My attempts

contourPotentialPlot1 = 
  ContourPlot[x + y - x y, {x, -5, 5}, {y, -5, 5}, Contours -> 15, 
   Axes -> False, PlotPoints -> 30, PlotRangePadding -> 0, 
   Frame -> False, ColorFunction -> "DarkRainbow"];

potential1 = 
  Plot3D[x + y - x y, {x, -5, 5}, {y, -5, 5}, ClippingStyle -> None, 
   Mesh -> None, ColorFunction -> Function[{x, y, z}, Hue[z]], 
   PlotTheme -> "Detailed"];
level = -40; gr = 
 Graphics3D[{Texture[contourPotentialPlot1], EdgeForm[], 
   Polygon[{{-5, -5, level}, {5, -5, level}, {5, 5, level}, {-5, 5, 
      level}}, 
    VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}, 
  Lighting -> "Neutral"];

Show[potential1, gr, PlotRange -> All, BoxRatios -> {1, 1, .6}, 
 FaceGrids -> {Back, Left}]

pts = Append[#, level] & /@ contourPotentialPlot1[[1, 1]];
cts = Cases[contourPotentialPlot1, Line[l_], Infinity];
cts3D = Graphics3D[GraphicsComplex[pts, {Opacity[.5], cts}]];
Show[potential1, cts3D, PlotRange -> All, BoxRatios -> {1, 1, .6}, 
 FaceGrids -> {Bottom, Back, Left}]

This is pretty good. Can this code be improved or modified?

Thanks for the help.

@PlatoManiac This gives a good result but z-axis is not equal — Emad kareem, Aug 23 '17 at 20:55

score 5 · Answer 1 · edited Aug 25 '17 at 14:29

In versions 10.2+, you can use SliceContourPlot3D

potential1 = Plot3D[x + y - x y, {x, -5, 5}, {y, -5, 5}, 
 ClippingStyle -> None, Mesh -> None, ColorFunction -> (ColorData["Rainbow"][#3] &), 
 PlotStyle -> Directive[Opacity[0.9]], PlotTheme -> "Detailed"];

We can use PlotRange[potential1] to get the x, y, and z ranges.

{xrange, yrange, zrange} = PlotRange[potential1];

contours = SliceContourPlot3D[x + y - x y, z == zrange[[1]], 
  {x, xrange[[1]], xrange[[2]]}, 
  {y, yrange[[1]], yrange[[2]]}, {z, zrange[[1]], zrange[[2]]}, 
  Contours -> 15,  PlotPoints -> 50, ColorFunction -> "TemperatureMap"];

Show[potential1, contours, 
  ImageSize -> 500, Lighting -> "Neutral", 
  PlotRange -> All, BoxRatios -> {1, 1, .6}, 
  FaceGrids -> {Back, Left}, ViewPoint -> {4, -4, 2}]

Update:

I need ContourPlot3D be transparent, Only curves appear

Use ContourShading -> None or ContourShading -> Opacity[0] (and remove ColorFunction-> "TemperatureMap") in SliceContourPlot3D to get

If I changed range of x,y∈[0,1] does not give the desired result

This is what I get when I use {x, 0, 1} and {y, 0, 1} in both Plot3D and SliceContourPlot3D:

Thank you so much , I need ContourPlot3D be transparent , Only curves appear — Emad kareem, Aug 23 '17 at 22:14
If I changed range of $ x , y \in [0,1]$ does not give the desired result — Emad kareem, Aug 23 '17 at 22:22

J. M.'s missing motivation · Answer 2 · 2017-08-27T01:45:34.867

Here is a method that uses only Plot3D[] with its MeshFunctions option, and achieves the desired result with a little post-processing:

p1 = Normal[Plot3D[x + y - x y, {x, -5, 5}, {y, -5, 5}, 
                   BoundaryStyle -> Directive[GrayLevel[2/3], AbsoluteThickness[1]], 
                   ClippingStyle -> None, ColorFunction -> "Rainbow", 
                   MeshFunctions -> {#3 &},
                   MeshStyle -> Directive[AbsoluteThickness[1.6], ColorData[97, 1]], 
                   PlotStyle -> Opacity[0.9], PlotTheme -> "Detailed"]];
tr = AffineTransform[{DiagonalMatrix[{1, 1, 0}], {0, 0, PlotRange[p1][[-1, 1]]}}];

p1 /. Line[l_] :> Line[tr @ l]

surface and projected contours

score 4 · Answer 3 · answered Aug 23 '17 at 21:24

To get the correct z-axis I will do just the following. I get the z-axis value from the PlotRange option of the Plot3D and set level to that value.

level = First@Last@(PlotRange /. AbsoluteOptions[potential1, PlotRange]);

All should be fine after that.

Updated version of your code:

contourPotentialPlot1 = 
  ContourPlot[x + y - x y, {x, -5, 5}, {y, -5, 5}, Contours -> 15, 
   Axes -> False, PlotPoints -> 30, PlotRangePadding -> 0, 
   Frame -> False, ColorFunction -> "TemperatureMap"];
potential1 = 
  Plot3D[x + y - x y, {x, -5, 5}, {y, -5, 5}, ClippingStyle -> None, 
   Mesh -> None, ColorFunction -> (ColorData["Rainbow"][#3] &), 
   PlotStyle -> Directive[Opacity[0.9]], PlotTheme -> "Detailed"];
level = First@
  Last@(PlotRange /. AbsoluteOptions[potential1, PlotRange]);
gr = 
 Graphics3D[{Texture[contourPotentialPlot1], EdgeForm[], 
   Polygon[{{-5, -5, level}, {5, -5, level}, {5, 5, level}, {-5, 5, 
      level}}, 
    VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}, 
  Lighting -> "Neutral"];
Show[potential1, gr, PlotRange -> All, BoxRatios -> {1, 1, .6}, 
 FaceGrids -> {Back, Left}]

Thank you so much. I have a question how to divide the axis period, for example, ${-5,-4,-2,...,4.5}$ — Emad kareem, Aug 23 '17 at 21:47
I need ContourPlot3D be transparent , Only curves appear, If I changed range of $ x , y \in [0,1]$ does not give the desired result — Emad kareem, Aug 23 '17 at 22:22

Emad kareem · Accepted Answer · 2017-08-24T01:18:50.400

This answer gives the result very close to the pictures in question depending on some of the answers

p1 = ContourPlot[x + y - x y, {x, 0, 1}, {y, 0, 1}, Contours -> 15, 
   ContourShading -> None];
p2 = Plot3D[x + y - x y, {x, 0, 1}, {y, 0, 1}, ClippingStyle -> None, 
   Mesh -> None, ColorFunction -> (ColorData["Rainbow"][#3] &), 
   PlotStyle -> Directive[Opacity[0.9]], 
   Ticks -> {{0, .1, .2, .3, .4, .5, .6, .7, .8, .9, 
      1}, {0, .1, .2, .3, .4, .5, .6, .7, .8, .9, 1}}, 
   ImageSize -> Large, PlotTheme -> "Detailed"];
level = First@Last@(PlotRange /. AbsoluteOptions[p2, PlotRange]);
gr = Graphics3D[{Texture[p1], EdgeForm[], 
    Polygon[{{{0, 0, 0}, {1, 0, 0}, {1, 1, 0}, {0, 1, 0}}}, 
     VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}, 
   Lighting -> "Neutral"];
pts = Append[#, level] & /@ p1[[1, 1]];
cts = Cases[p1, Line[l_], Infinity];
cts3D = Graphics3D[GraphicsComplex[pts, {Opacity[.5], {Blue, cts}}]];
Show[p2, cts3D, PlotRange -> All, BoxRatios -> {1, 1, .6}, 
 FaceGrids -> {{{0, 1, 0}, {Range[0, 1, 0.1], 
     Range[0, 1, 0.1]}}, {{-1, 0, 0}, {Range[0, 1, 0.1], 
     Range[0, 1, 0.1]}}, {{0, 0, -1}, {Range[0, 1, 0.1], 
     Range[0, 1, 0.1]}}}, ImageSize -> Large, PlotTheme -> "Detailed"]

How to plot a color consistently in Plot3D with 2D projection curve?

4 Answers4

Linked