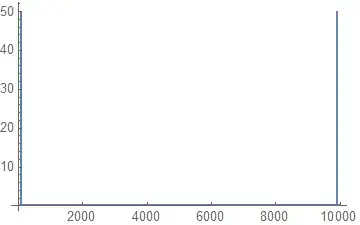
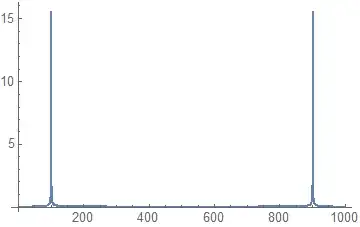
I am interested in evaluating the discrete Fourier transform for a list of data. The problem is the results given by the function Fourier depends on the length of the data.
For example, if the list of data is simply Table[Sin[20 π t], {t, 0, 10, x}] for different values of x I will obtain the same shape from Fourier when I plot the obtained numbers but the values on the $x$ axis will change.
For $x=0.001$ I will get:
But for $x=0.01$ I get:
The x axis of your plot has no meaning - it is simply the index of the value: The finer the data in your original table, the finer the frequency resolution and therefore the bigger the number of values in your output.
You can transform the axes however: The frequency spacing $\delta f$ and total bandwidth $\Delta f$ is defined the following way:
$\delta f=\frac{1}{\Delta t}$
$\Delta f=\frac{1}{\delta t},$
where $\delta t$ is the time domain spacing and $\Delta t$ is the total time span of the data.
Note: Despite the many duplicates (see comments), I thought it would be nice to have the relations written down somewhere without the need to extract them from code (as far as I could tell, they're not in any of the duplicates). It might be better to move this answer to one of the duplicates - if so, to which one should I move this?
