set colours for different parts of a piecewise function's graph

Question

I would like to create a graph of the piecewise function
$f(x) = \begin{cases} x + 2, & x < -1 \\ x^2, & -1 \leq x \leq 2 \\ 3, & x > 2\end{cases}$

where the changes in the definition of $f(x)$ are clearly demonstrated. Specifically, I would like to:

a) have each part of the definition graphed in a different colour;

b) have the appropriate open/closed disks (any simpler method than my tedious solution of plotting each disk?)

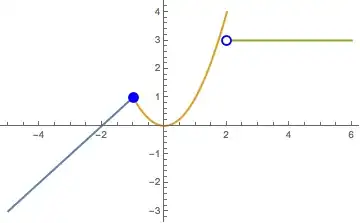
Here is what I have so far:

Plot[Piecewise[{{2+x,x<-1},{x^2,-1<x&&x<=2},{3,x>2}},0],{x,-5,6}, PlotStyle ->Thick, Epilog->{PointSize[0.03],Blue,Point[{-1,1}],PointSize[0.03],Blue,Point[{2,3}],PointSize[0.02],White,Point[{2,3}]}]

Which yields this:

Again, although this has the dots, it's a very tedious solution, and I would like to be able to set the colour of the three parts, separately (ideally have Mathematica do it automatically).

I am looking for a solution that students using a sandboxed version of Mathematica (provided through WolframAlpha Pro) could implement.

Answer 1

Plot[Piecewise[{#}, None] & /@ {{2 + x, 
     x < -1}, {x^2, -1 < x && x <= 2}, {3, x > 2}} // 
  Evaluate, {x, -5, 6}, PlotRange -> All,
 PlotStyle -> Thick, 
 Epilog -> {PointSize[0.03], Blue, Point[{-1, 1}], PointSize[0.03], 
   Blue, Point[{2, 3}], PointSize[0.02], White, Point[{2, 3}]}]

yields

Update: Demonstration of manual color manipulation. Also some minimalist conditioning around piecewise point graphics.

Specify conditions, e.g.:

conds = {{2 + x, x < -1}, {x^2, -1 < x && x <= 2}, {3, x > 2}};

and plot

Plot[
  Piecewise[{#}, None] & /@ conds // 
   Evaluate, {x, -5, 6}, PlotRange -> All,
  PlotStyle -> {{Thick, Red}, {Thick, Blue}, {Thick, 
     RGBColor[0.5, 0.19, 0.5]}}, 
 Epilog->Flatten[{PointSize[0.03], joinPiece[conds[[{1, 2}]], x], 
    joinPiece[conds[[{2, 3}]], x]}]]

yielding:

using the following minimal auto-formatting based on continuity (assuming region a < region b):

joinPiece[{a_, b_}, x_] := Module[{myVal},
   If[ (a[[1]] /. FindMaximum[{x, a[[2]]}, x][[2, 1]]) === (
      b[[1]] /. (myVal = FindMinimum[{x, b[[2]]}, x])[[2, 1]]
      ), {Blue, 
     Point[{myVal[[2, 1, 2]], a[[1]] /. myVal[[2, 1]]}]}, {White, 
     EdgeForm[{Thick, Blue}], 
     Disk[{myVal[[2, 1, 2]], b[[1]] /. myVal[[2, 1]]}, .15]}]];