Tangent Plane and Normal Vector

Question

I have this code that shows that the derivative is vertical to the surface. I need to change the point to an arrow that is vertical and moves as the point moves

f[x_, y_] = x + y - x y;
fx[x_, y_] = D[f[x, y], x];
fx[x_, y_] = Limit[(f[x + h, y] - f[x, y])/h, h -> 0];
fy[x_, y_] = D[f[x, y], y];
fy[x_, y_] = Limit[(f[x, y + h] - f[x, y])/h, h -> 0];
Manipulate[x0 = p[[1]]; y0 = p[[2]];
 Show[{Plot3D[{f[x, y], 
     f[x0, y0] + fx[x0, y0] (x - x0) + fy[x0, y0] (y - y0)}, {x, -5, 
     5}, {y, -5, 5}, BoxRatios -> {1, 1, 1}, 
    PlotRange -> {{-5, 5}, {-5, 5}, {-25, 25}}, 
    PlotStyle -> {Directive[Opacity[0.6]], 
      Directive[Orange, Opacity[0.6]]}, ViewPoint -> {2.5, -2, 1}, 
    ClippingStyle -> None], 
   Graphics3D[{PointSize[Large], 
     Point[{p[[1]], p[[2]], f[p[[1]], p[[2]]]}]}]}], {{p, {1, 
    1}}, {-1, -1}, {2, 2}}]

The change is so

I tried with the ِِArrow

Graphics3D[{Red, Arrowheads[0.1], 
  Arrow[Tube[{{1, 1, -1}, {2, 2, 0}, {3, 3, -1}, {4, 4, 0}}, 0.05]]}]

But I did not get the desired result.

Here here YouTube is aware of the way to use the Mathematica but did not display all the code.

it is better to define functions using := and not = unless you have specific reason to use = — Nasser, Sep 04 '17 at 05:18
Then, you should make up your mind and use either D[] or Limit[], but certainly not both. — J. M.'s missing motivation, Sep 04 '17 at 06:22
@Kuba Thank you very much. This also gives an approximate result, but Alexei's answer is correct. — Emad kareem, Sep 04 '17 at 14:54

score 3 · Accepted Answer · answered Sep 04 '17 at 07:55

For a lecture on differential geometry I did once a demonstration like you intend to (without a tangent plane though). May be it will be of some use to you. Here it is. I inserted the radius-vector that describes your surface. Please have a look.

 Manipulate[
 R0 = {xx, yy, 5 + (5 + xx + yy - xx*yy)/4};
 e1 = D[R0, xx];
 e2 = D[R0, yy];
 n = Cross[e1, e2]/Sqrt[e1.e1*e2.e2 - e1.e2^2];

 rule = {xx -> X, yy -> Y};
 Which[
  showR == False && showBasis == False && showN == False,
  Show[{
     Plot3D[R0[[3]] /. {xx -> x, yy -> y}, {x, -5, 5}, {y, -5, 5}, 
      PlotStyle -> Directive[Opacity[0.3]], Ticks -> None, 
      ViewPoint -> {13, -6, 5}, PlotRange -> All, Boxed -> False, 
      AxesOrigin -> {0, 0, 0}, ColorFunction -> "SunsetColors"],
     Graphics3D[{Text[Style["x", Italic, 16], {4.2, 0, 0.2}], 
       Text[Style["y", Italic, 16], {0.1, 2.4, 0.2}], 
       Text[Style["z", Italic, 16], {0, 0, 6.7}]}],
     Graphics3D[{PointSize[0.015], Point[R0], Point[{X, Y, 0}]}]
     }, BoxRatios -> Automatic] /. rule,

  showR == True && showBasis == False && showN == False,
  Show[{
     Plot3D[R0[[3]] /. {xx -> x, yy -> y}, {x, -5, 5}, {y, -5, 5}, 
      PlotStyle -> Directive[Opacity[0.3]], Ticks -> None, 
      ViewPoint -> {13, -6, 5}, PlotRange -> All, Boxed -> False, 
      AxesOrigin -> {0, 0, 0}, ColorFunction -> "SunsetColors"],
     Graphics3D[{Arrowheads[0.03], Thick, Blue, 
        Arrow[{{0, 0, 0}, R0}]}] /. rule,
     Graphics3D[{Text[Style["x", Italic, 16], {4.2, 0, 0.2}], 
       Text[Style["y", Italic, 16], {0.1, 2.4, 0.2}], 
       Text[Style["z", Italic, 16], {0, 0, 6.7}]}],
     Graphics3D[{Text[Style["R", Bold, Blue, 16], 
        Mean[{{0, 0, 0}, R0 + {1, 0, 0}}]], PointSize[0.015], 
       Point[R0], Point[{X, Y, 0}]}]
     }, BoxRatios -> Automatic] /. rule,

  showR == True && showBasis == True && showN == False,
  Show[{
     Plot3D[R0[[3]] /. {xx -> x, yy -> y}, {x, -5, 5}, {y, -5, 5}, 
      PlotStyle -> Directive[Opacity[0.3]], Ticks -> None, 
      ViewPoint -> {13, -6, 5}, PlotRange -> All, Boxed -> False, 
      AxesOrigin -> {0, 0, 0}, ColorFunction -> "SunsetColors"],

     Graphics3D[{Arrowheads[0.03], Thick, Blue, 
        Arrow[{{0, 0, 0}, R0}]}] /. rule,

     Graphics3D[{Text[Style["x", Italic, 16], {4.2, 0, 0.2}], 
       Text[Style["y", Italic, 16], {0.1, 2.4, 0.2}], 
       Text[Style["z", Italic, 16], {0, 0, 6.7}]}],

     Graphics3D[{Arrowheads[0.03], Thick, Red, 
        Arrow[{R0, R0 + Normalize[e1]}],
        Arrowheads[0.03], Arrow[{R0, (R0 + Normalize[e2])}]
        }] /. rule,

     Graphics3D[{Text[
        Style["\!\(\*SubscriptBox[\(e\), \(1\)]\)", Bold, Red, 
         16], {R0 + Normalize[e1] + {0.2, 0, 0}}], 
       Text[Style["\!\(\*SubscriptBox[\(e\), \(2\)]\)", Bold, Red, 
         16], {R0 + Normalize[e2] + {0, 0.2, 0}}], Red, 
       Text[Style["R", Bold, Blue, 16], 
        Mean[{{0, 0, 0}, R0 + {1, 0, 0}}]], PointSize[0.015], 
       Point[R0], Point[{X, Y, 0}]}]
     }, BoxRatios -> Automatic] /. rule,

  showR == True && showBasis == True && showN == True,
  Show[{
     Plot3D[R0[[3]] /. {xx -> x, yy -> y}, {x, -5, 5}, {y, -5, 5}, 
      PlotStyle -> Directive[Opacity[0.3]], Ticks -> None, 
      ViewPoint -> {13, -6, 5}, PlotRange -> All, Boxed -> False, 
      AxesOrigin -> {0, 0, 0}, ColorFunction -> "SunsetColors"],

     Graphics3D[{Arrowheads[0.03], Thick, Blue, 
        Arrow[{{0, 0, 0}, R0}]}] /. rule,

     Graphics3D[{Text[Style["x", Italic, 16], {4.2, 0, 0.2}], 
       Text[Style["y", Italic, 16], {0.1, 2.4, 0.2}], 
       Text[Style["z", Italic, 16], {0, 0, 6.7}]}],

     Graphics3D[{Arrowheads[0.03], Thick, Red, 
       Arrow[{R0, R0 + Normalize[e1]}],
       Arrowheads[0.03], Arrow[{R0, (R0 + Normalize[e2])}],
       Arrowheads[0.03], Darker@Green, Arrow[{R0, R0 + n}]
       }],

     Graphics3D[{Text[
        Style["\!\(\*SubscriptBox[\(e\), \(1\)]\)", Bold, Red, 
         16], {R0 + Normalize[e1] + {0.2, 0, 0}}], 
       Text[Style["\!\(\*SubscriptBox[\(e\), \(2\)]\)", Bold, Red, 
         16], {R0 + Normalize[e2] + {0, 0.2, 0}}], 
       Text[Style["n", Bold, Darker@Green, 
         16], {R0 + n + {0, 0, 0.2}}], 
       Text[Style["R", Bold, Blue, 16], 
        Mean[{{0, 0, 0}, R0 + {1, 0, 0}}]], PointSize[0.015], 
       Point[R0], Point[{X, Y, 0}]}]



     }, BoxRatios -> Automatic] /. rule


  ],

 Column[{
   Row[{Control[{{X, 1.7}, 0, 4}], Spacer[30], 
     Control[{{Y, 0}, -2, 2}]}],
   Row[{
     Control[{{showR, False}, {True, False}}], Spacer[30], 
     Control[{{showBasis, False}, {True, False}}], Spacer[30],
     Control[{{showN, False}, {True, False}}]}]

   }, Alignment -> Center], 
 ControlType -> {Slider, Slider, Checkbox, Checkbox, Checkbox}

    SaveDefinitions -> True]

To see the vectors check the check boxes. The green arrow shows the unit normal vector, the red ones the tangent unit vectors. It should look like the following:

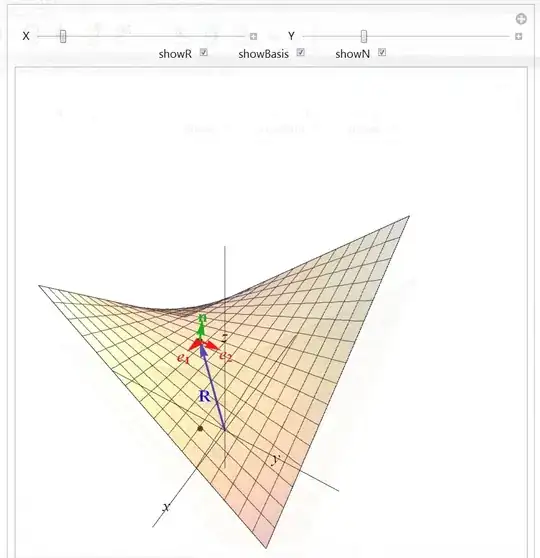
Have fun!

Thank you very much. This helps me a lot, are you studying differential geometry. — Emad kareem, Sep 04 '17 at 09:40
@Emad kareem No. Differential geometry was a small part of the course of lectures on biomembranes I gave. — Alexei Boulbitch, Sep 04 '17 at 11:05
Thank you so much. This helped me a lot. I am grateful to you. — Emad kareem, Sep 04 '17 at 14:58

Tangent Plane and Normal Vector

1 Answers1