Is there a way to use functions like Prime[n] within Solve[]?

Question

I'm trying to see if a number can be written as the sum of two prime numbers. Ideally, I would like to use

Solve[ Prime[n] + Prime[m] == 100, {n, m}]

But that simply doesn't work in Mathematica.

So is there another way to implement this?

Answer 1

If not assumed otherwise m and n can be whatever, so you can do e.g. this :

Solve[ Prime[n] + Prime[m] == 100, {n, m}, Integers]

{{n -> 2, m -> 25}, {n -> 5, m -> 24}, {n -> 7, m -> 23}, {n -> 10, m -> 20}, 
 {n -> 13, m -> 17}, {n -> 15, m -> 16}, {n -> 16, m -> 15}, {n -> 17, m -> 13}, 
 {n -> 20, m -> 10}, {n -> 23, m -> 7}, {n -> 24, m -> 5}, {n -> 25, m -> 2}}

or in a different (and much better) way :

PrimePi @ {n, m} /. Solve[n + m == 100, {n, m}, Primes]

PrimePi and Prime are Listable.

Edit

Since there are many ways in Mathematica to solve problems I add another one :

PrimePi @ Select[ FrobeniusSolve[ {1, 1}, 100], And @@ PrimeQ @ # &]

{{ 2, 25}, { 5, 24}, { 7, 23}, {10, 20}, {13, 17}, {15, 16},
 {16, 15}, {17, 13}, {20, 10}, {23, 7 }, {24, 5 }, {25, 2 }}

This way is competitive because FrobeniusSolve is much faster than Solve or Reduce, I recommend to take a look at this answer for an interesting comparison.

Edit 2

To compare efficency of two Solve approches, let's evaluate :

sp = Table[{k, PrimePi @ {n, m} /. Solve[n + m == 100 k, {n, m}, Primes]; // AbsoluteTiming
            // First}, {k, 20}];
si = Table[{k, Solve[ Prime[n] + Prime[m] == 100 k, {n, m}, Integers]; // AbsoluteTiming 
           // First}, {k, 20}];

using a new (in Mathematica 9) option PlotLegends :

ListPlot[ Tooltip @ {sp, si}, PlotMarkers -> {Automatic, Medium}, AspectRatio -> 1/2,
          AxesLabel -> {k, "timings"}, Joined -> True, PlotLegends -> 
          Placed[{ Style["Solve over the Primes", Large], 
                   Style["Solve over the Integers", Large]}, {Right, Center}],
          ImageSize -> 700]

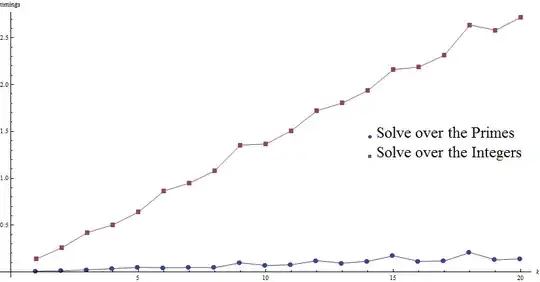
Timings are roughly 20 times better for solving over the primes :

si[[18 ;;]]
sp[[18 ;;]]

{{18, 2.582000}, {19, 2.571000}, {20, 2.707000}}
 {18, 0.207000}, {19, 0.127000}, {20, 0.142000}}

Now, let's compare Solve over the primes and FrobeniusSolve approach. Instead of Select[...] we take Cases[...] (suggested by Rojo in the comments) since the latter appears to be slightly faster.

spp = Table[{k, PrimePi @ {n, m} /. Solve[n + m == 500 k, {n, m}, Primes];
             // AbsoluteTiming // First}, {k, 20}];
cfs = Table[{k, PrimePi @ Cases[ FrobeniusSolve[{1, 1}, 500 k], {_?PrimeQ ..}]; 
            // AbsoluteTiming // First}, {k, 20}];

ListPlot[ Tooltip @ {cfs, spp}, PlotMarkers -> {Automatic, Large}, AspectRatio -> 1/2, 
          PlotLegends -> Placed[{ Style["Cases and FrobeniusSolve", 30], 
                                  Style["Solve over the Primes", 30]}, Right], 
          Joined -> True, AxesLabel -> {k, "timings"}, ImageSize -> 700]

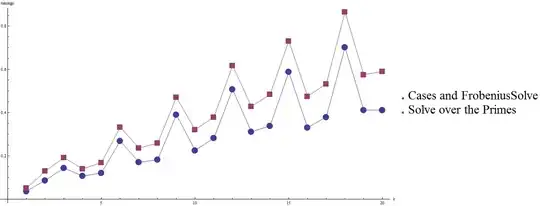
We can see that timings for FrobeniousSolve are roughly 20-40 % better than for the Solve over Primes approach :

cfs[[18 ;;, 2]]
spp[[18 ;;, 2]]

{0.702000, 0.412000, 0.412000}
{0.866000, 0.576000, 0.591000}

The larger numbers we deal with the better is the FroneniousSolve approach. This issue is even clearer if we have more variables.
The oscillating pattern of the above plots of timings is coupled to the number of prime solutions $(m, n)$ to this equation $m + n = k\;$ for any integer $k$.

Answer 2

You can do :

Reduce[Prime[n] + Prime[m] == 100, {n, m}, Integers]