This is a bit of a shot in the dark, as your actual goal is a little opaque.
To figure things out, start with a smaller list:
SeedRandom[1];
jj = RandomReal[{-1, 1}, 10];
Notice that
Clear[a]
a^2 jj
(* {0.634779 a^2, -0.777161 a^2, 0.579052 a^2, -0.624394 a^2, -0.517278 a^2,
-0.868522 a^2, 0.0844932 a^2, -0.537691 a^2, -0.207988 a^2, 0.400948 a^2} *)
That is, if you want to multiply a list by a number, you can just multiply a list by a number. So, perhaps you want:
y1 = Transpose[{a^2 jj, a jj}];
y2 = Transpose[{a jj, (a^3 + 4) jj}];
(* y1 = {{0.634779 a^2, 0.634779 a}, {-0.777161 a^2, -0.777161 a}, {0.579052 a^2, 0.579052 a},
{-0.624394 a^2, -0.624394 a}, {-0.517278 a^2, -0.517278 a}, {-0.868522 a^2, -0.868522 a},
{0.0844932 a^2, 0.0844932 a}, {-0.537691 a^2, -0.537691 a}, {-0.207988 a^2, -0.207988 a},
{0.400948 a^2, 0.400948 a}} *)
So y1 and y2 are lists of pairs generated from your random numbers by the specified formulae.
I will assume you want to plot these points for some value of a:
ListPlot[{y1, y2} /. a -> 0.5]
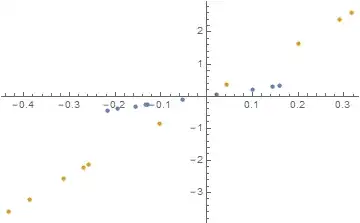
There are more concise ways of doing this, if you so wish. I would strongly encourage you to thoroughly read the documentation of any interesting looking functions and play with the examples therein. Most things are probably much easier than you think they'll be.

jis overridden immediately in theForloop? Also, the loop just overridesyover and over. And finally, theTablestatement in the last line also does nothing interesting, since nothing depends onj. (look atx1/x2) – Lukas Lang Sep 11 '17 at 08:05Forloop.You are right aboutTableas I mentioned. – user31694 Sep 11 '17 at 08:47For[n = 1, n <= 1000, n++, y = {{a^2*j[[n]], a*j[[n]]}, {a*j[[n]], (a^3 + 4)*j[[n]]}};];– Sumit Sep 11 '17 at 09:43Forloop" - no, they are not. In the loop,jis an iterator that goes from 1 to 1000. Period. Your random numbers, as defined in the first line, arej[[1]]as the first element,j[[2]]as the second, ...,j[[i]]as the ith. Maybe you want something like:For[i=1,i<=1000,i++, y={{a^2*j[[i]],a*j[[i]]},{a*j[[i]],(a^3+4)*j[[i]]}}; ]? But note thatyis just{{0.0867359 a^2, 0.0867359 a}, {0.0867359 a, 0.0867359 (4 + a^3)}}... If you want a list of suchys applied to each random numberj[[i]], just do: (....) – corey979 Sep 11 '17 at 09:47Table[{{a^2 j[[i]], a j[[i]]}, {a j[[i]], (a^3 + 4) j[[i]]}}, {i, 1, 1000}]or simply{{a^2 #, a #}, {a #, (a^3 + 4) #}} & /@ j. See also Why should I avoid the For loop in Mathematica? – corey979 Sep 11 '17 at 09:48Forin your example, evenjj*{{a^2,a},{a,a^3+4}}would work here since every element is simply multiplied byjj[k]. And to repeat: You just assign a new value toyin every iteration of the loop in your current code – Lukas Lang Sep 11 '17 at 11:14