Depth first scan of a tree backwards

Question

How can I traverse this tree, to get a sequence of vertices {8,4,2,9,5,1,6,3,7}? I've failed to produce it with DepthFirstScan, does this particular order even has a name?

TreeGraph[{1->2,1->3,2->4,2->5,3->6,3->7,4->8,5->9}, VertexLabels -> "Name"]

Which algorithm did you use to produce this order or the vertices? — A.G., Sep 11 '17 at 18:21
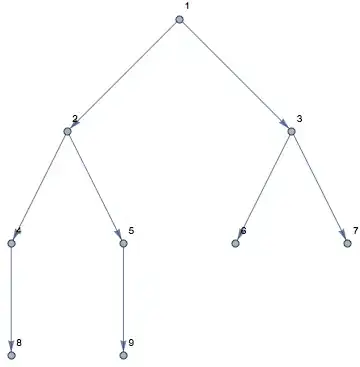
You can get pretty close using DepthFirstScan and the "PostvisitVertex" event - are you sure that's not what you want? Your order seems a bit strange, given that e.g. 2 is visited between visiting the two subbranches — Lukas Lang, Sep 11 '17 at 18:58
@A.G. I don't know what's the algorithm is called, but it outputs the vertices while backtracking backwards from DFS. — swish, Sep 11 '17 at 20:40
@swish As I understand a vertex is listed when the DFS has exhausted its adjacency list. If that is correct, node "1" should be last in the list. Is that correct? — A.G., Sep 11 '17 at 22:16
i am sure this is not what you want, but it does give {8,4,2,9,5,1,6,3,7}: rubeGoldbergSort[g_] := SortBy[VertexList[g], {PropertyValue[{g, #}, VertexCoordinates] &}]; rubeGoldbergSort@ TreeGraph[{1 -> 2, 1 -> 3, 2 -> 4, 2 -> 5, 3 -> 6, 3 -> 7, 4 -> 8, 5 -> 9}, VertexLabels -> "Name"]:) — kglr, Sep 12 '17 at 08:33
@kglr Suprisingly it also gives the right answer for a bigger tree graph I have, so it probably not a coincidence and this sort function is indeed traverses the tree the way I want it to, thx :) — swish, Sep 12 '17 at 12:08
swish, but this depends only on the layout. I was assuming the sequence was generated by something more subtle. — kglr, Sep 12 '17 at 12:21
@kglr I'm also unaware of the original method, outputing vertices on backward motion of DFS was just a guess. But coordinate sort on default layout is apparently does the same thing. — swish, Sep 12 '17 at 12:50

score 1 · Answer 1 · answered Sep 12 '17 at 07:57

As noted in the comments, the following gets you close:

g = TreeGraph[{1->2,1->3,2->4,2->5,3->6,3->7,4->8,5->9}, VertexLabels -> "Name"]

Reap[DepthFirstScan[g, 1, {"PostvisitVertex" -> Sow}]][[2, 1]]
(* {8, 4, 9, 5, 2, 6, 7, 3, 1} *)

The difference between this and your order is that a vertex is only visited after all subbranches have been visited. (whereas your order lists them after the first subbranch, which seems a bit arbitrary)

score 1 · Accepted Answer · answered Sep 12 '17 at 21:00

Based on swish's comment ("Suprisingly it also gives the right answer for a bigger tree graph I have, so it probably is not a coincidence and this sort function is indeed traverses the tree the way I want it to"), perhaps:

coordinateSort[g_] := SortBy[VertexList[g], PropertyValue[{g, #}, VertexCoordinates]&]; 

coordinateSort@TreeGraph[{1 -> 2, 1 -> 3, 2 -> 4, 2 -> 5, 3 -> 6, 3 -> 7, 4 -> 8, 5 -> 9}]

{8, 4, 2, 9, 5, 1, 6, 3, 7}

Depth first scan of a tree backwards

2 Answers2