How to plot the 3D-boundary of California or other states

Question

I can get the postion with this code

pos = First[
  Flatten[#, 1] & /@ 
   First[Entity[
      "AdministrativeDivision", {"California", "UnitedStates"}][
     EntityProperty["AdministrativeDivision", "Polygon"]]]]

You can see the postion in the map

GeoListPlot[GeoPosition[pos]]

Mathematica graphics

I can get their elevation

eleData = 
 QuantityMagnitude[
  GeoElevationData[
   Flatten[#, 1] & /@ 
    First[Entity[
       "AdministrativeDivision", {"California", "UnitedStates"}][
      EntityProperty["AdministrativeDivision", "Polygon"]]]]]

Then I get the data

data = Flatten /@ Transpose[{pos, List /@ eleData}]

I can plot its discrete plot

ListPointPlot3D[data]

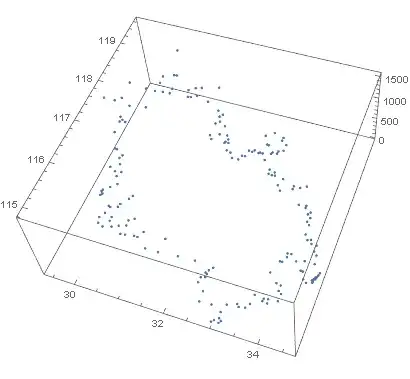
Mathematica graphics

But how to connected those discrete points to get a smooth boundary?

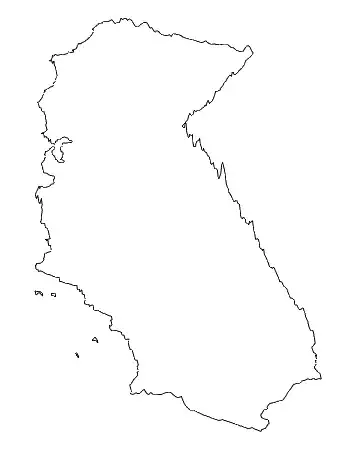
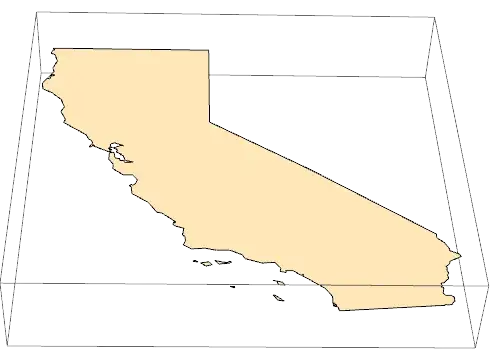
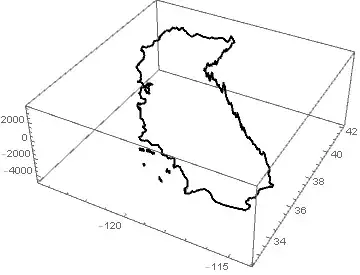
If the points are returned in order, you could try ListLinePlot[pos]. The islands might cause a few problems. — QuantumDot, Sep 17 '17 at 12:45
Some answers do essentially the same thing here, but with countries instead of a single state. Somewhat related: (60427) — Michael E2, Sep 17 '17 at 13:24
@MichaelE2 Thanks for the links,but in my case,I just want to get the boundary — yode, Sep 17 '17 at 13:43
Yep, and that's what the answer in the question does. ("Wireframe": just change to FaceForm[None] or change Polygon to Line and append the first point(s) to the end(s).) — Michael E2, Sep 17 '17 at 13:52

score 6 · Answer 1 · answered Sep 17 '17 at 18:04

Here's another (slightly hacky) approach. The idea is to take the BoundaryMeshRegion from GeoElevationData, take only the top, then take the topological boundary.

First the BoundaryMeshRegion:

cali = Entity["AdministrativeDivision", {"California", "UnitedStates"}];
reg = GeoElevationData[cali, Automatic, "Region"]

To get the top portion of this region, I select the primitives free of a coordinate that's at the bottom of the region:

floor = RegionBounds[reg][[3, 1]];
prims = Select[MeshPrimitives[reg, 2], FreeQ[floor]];

Visualize this:

DiscretizeGraphics[prims]

I then tally the each line segment of each triangle and select the ones with multiplicity one. This will give me the boundary:

segs = Catenate[Partition[#, 2, 1, 1] & /@ prims[[All, 1]]];
boundary = Cases[Tally[Sort /@ segs], {_, 1}][[All, 1]];

To visualize, I exaggerate the z box ratio, assuring the xy ratios are to scale:

ratio = Divide @@ Most[Subtract @@@ RegionBounds[reg]];
Graphics3D[Line[segs], BoxRatios -> {1, ratio, .1}, Boxed -> False]

Ah, I was trying to separate out the islands with ConnectedMeshComponents[], but my machine hung. :o Nice solution! — J. M.'s missing motivation, Sep 17 '17 at 18:43

score 5 · Answer 2 · answered Sep 17 '17 at 13:53

5

As you geo-polygon has the 2D coordinates you need. However, the coordinate system ofGraphics and GeoGraphics are not the same. You need to Reverse the geo-polygon coordinate pairs to make them compatible in graphics. The GeoPosition head must also be removed. Finally a z-axis coordinate should be added (I used MapAt) for the polygon in Graphics3D.

With

geoPoly = 
 Entity["AdministrativeDivision", {"California", "UnitedStates"}][
  EntityProperty["AdministrativeDivision", "Polygon"]]

Then

Graphics3D@
 MapAt[Append[0], {All, All, All}]@
  Reverse[geoPoly /. GeoPosition -> Identity, 4]

Mathematica graphics

Hope this helps.

answered Sep 17 '17 at 13:53

Edmund

42,267
3
51
143

I'm sorry I missed the elevation data information in my original post..That so sorry..But I have updated it. – yode Sep 17 '17 at 14:01
EntityValue[ Entity["AdministrativeDivision", {"California", "UnitedStates"}], EntityProperty["AdministrativeDivision", "Polygon", {"ZoomLevel" -> 9}]] get better result – yode Sep 17 '17 at 16:41

score 5 · Answer 3 · answered Sep 17 '17 at 13:59

5

Here's one possible method:

california = Entity["AdministrativeDivision", {"California", "UnitedStates"}];

bounds = GeoBounds[california];
cheights = Reverse[QuantityMagnitude[GeoElevationData[Transpose[bounds],
                                                      GeoZoomLevel -> 4,
                                                      UnitSystem -> "Metric"]]];
crf = RegionMember[MapAt[Map[Reverse[#, 2] &, QuantityMagnitude[LatitudeLongitude[#]]] &, 
                         EntityValue[california, "Polygon"], 1]];

ListPlot3D[cheights, BoundaryStyle -> Thick, DataRange -> Reverse[bounds],
           Mesh -> None, PlotStyle -> None, RegionFunction -> (crf[{#1, #2}] &)]

3D boundary of California

Use Cases[] as usual if you need the actual Line[] objects.

answered Sep 17 '17 at 13:59

J. M.'s missing motivation

124,525
11
401
574

I'm sorry I missed the elevation data information in my original post..That so sorry..But I have updated it. – yode Sep 17 '17 at 14:02
That's OK; I got what you meant, as you can see from the figure in this answer. – J. M.'s missing motivation Sep 17 '17 at 14:03
Yes,it is indeed. – yode Sep 17 '17 at 14:10
Could we have any fast solution?I like your result but I have to say to get that cheights will cost too many time.. – yode Sep 17 '17 at 14:40
@yode - "fast" in this case also means "low resolution"; that would be the equivalent of just mapping GeoElevationData[] on the boundary points of the region, which is similar to what you did in the OP. – J. M.'s missing motivation Sep 17 '17 at 14:52
Actually I want to get all state bounday in a USA map.But maybe my internet too bad to get those curated data – yode Sep 17 '17 at 15:02
@yode, yes, that'd be hard to do, especially under the Great Firewall. (FWIW, my Internet is also slow, and it took me eight tries before cheights returned the expected QuantityArray[].) – J. M.'s missing motivation Sep 17 '17 at 15:04
1

EntityValue[ Entity["AdministrativeDivision", {"California", "UnitedStates"}], EntityProperty["AdministrativeDivision", "Polygon", {"ZoomLevel" -> 8}]] get better result.And more fast. – yode Sep 17 '17 at 16:39
Ah! I didn't know that can take a "ZoomLevel" setting! I'll try that later, as I'm busy with something else at the moment. – J. M.'s missing motivation Sep 17 '17 at 16:43

score 4 · Accepted Answer · answered Sep 17 '17 at 18:38

Another approach is similar to Yode's answer, but to refine the boundary into smaller segments before calling GeoElevationData.

poly = EntityValue[
  Entity["AdministrativeDivision", {"California", "UnitedStates"}], 
  "Polygon"
] /. GeoPosition -> Identity;

Refine the boundary by imposing a maximum length:

bd = DiscretizeRegion[RegionBoundary[poly], MaxCellMeasure -> {1 -> .1}];

Now replace each 2D coordinate with it's 3D version. Here we make one bulk call to GeoElevationData to avoid the overhead of many server calls:

raw = GeoElevationData[GeoPosition[MeshCoordinates[bd]], Automatic, "GeoPosition"];
pts3D = First[raw][[All, {2, 1, 3}]];

Now we construct a MeshRegion (or equivalently we could use Graphics3D + GraphicsComplex):

ratio = Divide @@ Subtract @@@ RegionBounds[bd];
MeshRegion[pts3D, MeshCells[bd, 1], BoxRatios -> {ratio, 1, .1}]

score 1 · Answer 5 · answered Sep 17 '17 at 16:51

1

Considering the J.M and Edmund's answer,I figure out more faster method based on Entity

poly = EntityValue[
    Entity["AdministrativeDivision", {"California", "UnitedStates"}], 
    EntityProperty["AdministrativeDivision", 
     "Polygon", {"ZoomLevel" -> 6}]] /. GeoPosition -> Identity;
shape = MapAt[
   Append[Reverse[#], QuantityMagnitude[GeoElevationData[#]]] &, 
   poly, {All, All, All}];
Graphics3D[{FaceForm[], shape}, BoxRatios -> {1, 1, 1/3}]

answered Sep 17 '17 at 16:51

yode

26,686
4
62
167

1

So you don't want the real spatial configuration, but one where sea-level is assumed to be flat and lines of longitude are assumed to be parallel? (The non-flat coastline in the graphics is, I assume, due to numerical error in the data. That's not what I'm asking about. The coast viewed from the side should show the earth's curvature and not be roughly level.) – Michael E2 Sep 17 '17 at 17:14

How to plot the 3D-boundary of California or other states

5 Answers5