I am new to Mathematica and I am trying to create the electric field $F$ from the electric potential $V$ (using arbitrary distances) and then plot the subsequent vector graph to show that the electric field is always pointing away from the point source.
So far I have:
Clear["Global`*"]
(* Creating the Vector Potential V using the Blank operator *)
V[p_, r_] = q/Times[4*Pi*ϵ*Norm[r - p]];
V[{Subscript[x, 1], Subscript[y, 1], Subscript[z, 1]}, {x, y, z}] //
TraditionalForm;
(* Creating the Electric Field F using the derivative of the Vector \
Field V *)
F[{x1_, y1_, z1_}] = -D[V[{x1, y1, z1}, {x, y, z}], {{x, y, z}}] /.
Derivative[1][Abs][x_] :> x/Sqrt[x^2] // TraditionalForm;
(* Setting the charge q and the constant ϵ *)
q = 1; ϵ = 1;
(* Creating the VectorPlot3D *)
v = VectorPlot3D[F[{1, 1, 1}], {x, -6, 6}, {y, 0, 4}, {z, -4, 4},
VectorStyle -> "Arrow3D", VectorPoints -> 5,
VectorScale -> {0.3, Scaled[0.3]}]
But when I run this I don't get any graph.
I've even found an example on Mathematica that doesn't work when I try to run it. Any help would be appreciated!

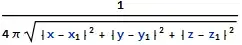
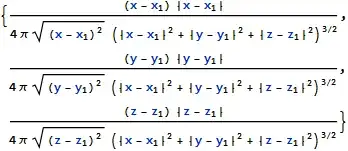
// TraditionalFormfrom the definition ofF. (TradtionalFormis meant for output only, not for something that will be used later in a computation.) – jjc385 Sep 18 '17 at 13:04