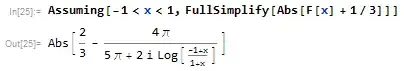By experiments, I am expecting that the following complex function
G[z_] := I*(1 - z)/(1 + z);
G2[z_] := z/(2 Pi I) - 1;
G3[z_] := -1 - 1/z;
F[z_] := G3[G2[Log[G[z]]]];
should work the same as the one in this question, namely, mapping the interval $(-1,1)$ to the boundary of the open ball $B_{2/3}(-1/3)$. I have checked it numerically:
Rationalize[Abs[F[RandomReal[{-1, 1}, 10]] + 1/3]]
which gives the desired result $2/3$. But I want to check it symbolically as well and I used the code from this answer:
Assuming[-1 < x < 1, FullSimplify[Abs[F[x] + 1/3]]]
which gives
Why does the Assuming function not work in this case? How can I fix it?
