How do I plot multiple plots with recurring functions more efficiently?

Question

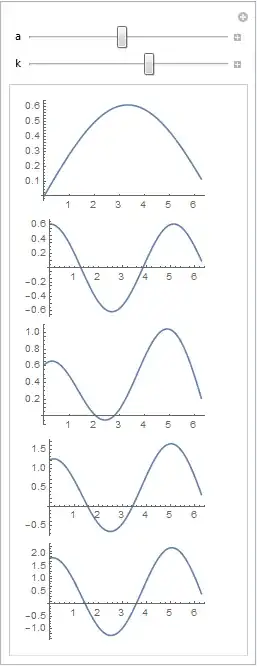
I want to manipulate multiple plots with recurring functions, take for example:

Manipulate[Grid[{
   {Plot[f1 = a*Sin[k*x], {x, 0, 2 Pi}]},
   {Plot[f2 = a*Cos[2 k*x], {x, 0, 2 Pi}]},
   {Plot[f1 + f2, {x, 0, 2 Pi}]},
   {Plot[f1 + 2 f2, {x, 0, 2 Pi}]},
   {Plot[f1 + 3 f2, {x, 0, 2 Pi}]}}],
 {a, 0, 1}, {k, 0, 1}]

The functions of the last three plots are composed of the two functions in the first two plots (which I have named f1 and f2). But when I evaluate in the above way the last three do not turn out correctly. They only do when I enter f1 and f2 in their complete forms, which I believe causes redundant repetitions of f1 and f2, and takes an increasingly heavy toll whence I plot complicated functions. Is there a more efficient way?

Answer 1

Your definition of f1 and f2 is wrong, it calculates once at the first. Let's defines them as functions:

f1 = #1*Sin[#2*#3] &;
f2 = #1*Cos[2 #1*#3] &;

Manipulate[Grid[{
   {Plot[f1[k, a, x], {x, 0, 2 Pi}]},
   {Plot[f2[k, a, x], {x, 0, 2 Pi}]},
   {Plot[f1[k, a, x] + f2[k, a, x], {x, 0, 2 Pi}]},
   {Plot[f1[k, a, x] + 2 f2[k, a, x], {x, 0, 2 Pi}]},
   {Plot[f1[k, a, x] + 3 f2[k, a, x], {x, 0, 2 Pi}]}}], {a, 0, 1}, {k,
   0, 1}]