Is it possible to get a cross-section along an axis for ConvexHullMesh

Question

Is it possible to get a cross-section along an axis for ConvexHullMesh? I've previously done it using RegionPlot for an equation, but am not sure how to do it for a list of values.

Previously I had an equation and used RegionPlot, but for this new analysis I have a set of data in a list in the format {x,y,z} that I'm visualising using ConvexHullMesh, and I'm trying to find a way to get a 2d cross-section along a specific point along the x, y or z axis. I was unable to adapt the RegionPlot solution since the previous solution relied on an equation instead of a list of points.

Previous code that could not be adapted for ConvexHullMesh:

plot2dz0[f_, range_, contour_, opt : OptionsPattern[], mod_] := RegionPlot[  
Evaluate[Abs[f[mod*r, \[Theta], \[Phi]] /. sphericalToCartesian]^2 > 
contour] /. z -> 0, {x, -range, range}, {y, -range, range}, PlotRange -> 
{{-1, 1}, {-1, 1}}]

I have gotten something workable in part by adapting from here. Would this be the best solution?

testdata = Flatten[RandomReal[{0, 1}, {3, 3, 3}], 1];

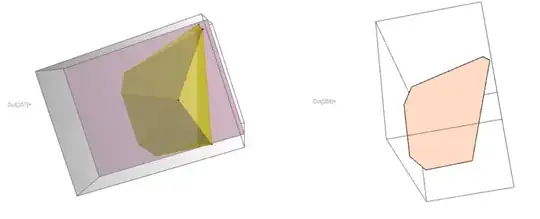
testPlot1 = ConvexHullMesh[%];

plane = InfinitePlane[{{1, 0, 1}, {1, 0, 0}, {1, 1, 1}}];

Show[Graphics3D[plane], testPlot1]

crossSection = RegionIntersection[plane, #] & /@ MeshPrimitives[testPlot1, 2] // DeleteCases[_EmptyRegion] // ReplaceAll[Line :> Sequence] // Flatten[#, 1] & // (#[[Last@FindShortestTour[#]]] &) // Polygon;

Graphics3D[crossSection]

Previously I had an equation and used RegionPlot, but for this new analysis I have a set of data in a list in the format {x,y,z} that I'm visualising using ConvexHullMesh, and I'm trying to find a way to get a 2d cross-section along a specific point along the x, y or z axis. I was unable to adapt the RegionPlot solution since the previous solution relied on an equation instead of a list of points. — Letshin, Oct 01 '17 at 22:18
I made some edits and have done some additional work on it as well, and so have updated the question to reflect that. — Letshin, Oct 01 '17 at 22:46
What's "best" here depends on what you need. If you just need the visual you can use ClipPlanes and Show and that might be easier. — b3m2a1, Oct 01 '17 at 22:48
Yes, just a way to visualise the cross-section is all that is needed at the moment. I will try that. What seems to be a problem is that for some planes I am getting an "...expression... cannot be used as a part specification" error. — Letshin, Oct 01 '17 at 22:54
I would love to see a solution that produces a true region as the output! — Szabolcs, Oct 02 '17 at 09:30

score 6 · Answer 1 · answered Oct 02 '17 at 03:56

Here's one quick possibility:

BlockRandom[SeedRandom[42]; (* for reproducibility *)
            testdata = Flatten[RandomReal[1, {3, 3, 3}], 1]];
chm = ConvexHullMesh[testdata];
plane = {1, -1, 2}.({x, y, z} - {1/4, -1/5, 1/3}) == 0;

Show[SliceContourPlot3D[1, plane, {x, y, z} ∈ chm], 
     BoundaryMeshRegion[chm, MeshCellStyle -> {{2, All} -> Opacity[1/4]}]]

slice of a convex hull

score 4 · Accepted Answer · answered Oct 02 '17 at 00:06

So here are two quick ways to do this.

If you're mostly interested in just viewing the cut-out, use ClipPlanes:

hullData = Flatten[RandomReal[{0, 1}, {3, 3, 3}], 1];
hullMesh = ConvexHullMesh[%];

planeNormal = Normalize@{0, 0, 1};
{planeVec1, planeVec2} = NullSpace[{planeNormal}];
planeCenter = Mean /@ CoordinateBounds@hullData;
plane = InfinitePlane[planeCenter, {planeVec1, planeVec2}];

Show[
 hullMesh,
 ClipPlanes -> plane,
 ClipPlanesStyle -> Directive[Red, Opacity[.25]]
 ]

Alternately you can build a new region by intersecting with an extrusion of the plane:

diam = 1.5*Abs[Subtract @@ MinMax@Flatten@CoordinateBounds@hullData];
planeRegion =
  Parallelepiped[
   planeCenter - diam*(planeVec1 + planeVec2)/2,
   {
    diam*planeVec1,
    diam*planeVec2,
    planeNormal
    }
   ];

Show[
 RegionIntersection[
  hullMesh,
  planeRegion
  ],
 Graphics3D[
  {
   Directive[Red, Opacity[.25]],
   plane
   }
  ]
 ]

Thanks, one question is if there is any possibility of plotting the perimeter of the cross-section as a 2D plot? I managed to do this in Mathematica 11.0 but the solution shown in the post is broken for 11.2, unfortunately. — Letshin, Oct 03 '17 at 09:06

Is it possible to get a cross-section along an axis for ConvexHullMesh

2 Answers2