3D plot of multiple functions

Question

I am just starting to learn Mathematica. I defined two functions

Subscript[x, 1][t_, α_] :=1/2 (3 - 2 E^-t + E^t (2 + t) (-1 + α) - α)

And

Subscript[x, 2][t_, α_] :=1 - 2 E^-t - E^t (2 + t) (-1 + α) + α

I ploted the followings

Plot[{Subscript[x, 1][t, 0], Subscript[x, 2][t, 0]}, {t, 0, 8}]
Plot[{Subscript[x, 1][5, α], 
  Subscript[x, 2][5, α]}, {α, 0, 1}]

My problem is that I want these two plots in 3D plot such that graphics of x1(t,0) and x2(t,0) are on the xy-plane and graphs of x1(2,alpha) and x2(2,alpha) lie on them forming a triangular shape in 3D. Sorry for my english I hope I could explain myself....

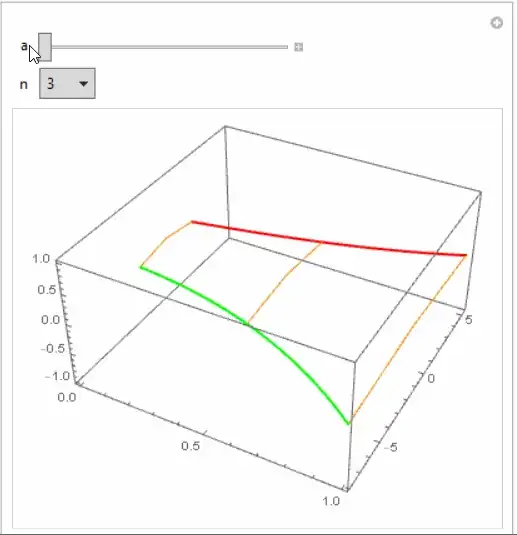
What do you mean by "lie on them"? Do you want to plot the curves of your function inside a plot with axes t,α and x? If so, take a look at ParametricPlot3D — Lukas Lang, Oct 04 '17 at 11:42
Plot3D[{Subscript[x, 1][t, \[Alpha]], Subscript[x, 2][t, \[Alpha]]}, {t, 0, 2}, {\[Alpha], 0, 1}, ClippingStyle -> None] — Bob Hanlon, Oct 04 '17 at 13:01
Thanks for your replay. I added a sketch to explain myself better. — bluehills, Oct 04 '17 at 18:48
There's been so many questions with Subscript definitions lately. I have an urge to close them all, referring askers to this, this, this, and this. — LLlAMnYP, Oct 05 '17 at 08:22
I edited the image link back into the post, since you had a reference to it. I assumed it was mistakenly removed. — Michael E2, Oct 06 '17 at 10:38

score 5 · Answer 1 · answered Oct 05 '17 at 09:34

5

Perhaps this can be motivating:

f[t_] := {t, 1/2 (3 - 2 E^(-t) + E^t (2 + t) ), 0}
g[t_] := {t, 1 - 2 E^-t - E^t (2 + t), 0}
h[a_, n_] := 
 Table[Line[{f[j], Mean[{f[j], g[j]}] + {0, 0, a}, g[j]}], {j, 0, 1, 
   1/(n - 1)}]
Manipulate[
 Show[ParametricPlot3D[{f[u], g[u]}, {u, 0, 1}, 
   PlotStyle -> {Red, Green}], Graphics3D[{Orange, h[a, n]}], 
  BoxRatios -> {2, 2, 1}], {a, 0.1, 1}, {n, Range[3, 10]}]

answered Oct 05 '17 at 09:34

ubpdqn

60,617
3
59
148

Yes, ıt is almost what I need but the important point is the left side of the triangle must be the graph of the function x1(5, alpha) and the right side is the graph of the function x2(5, alpha). – bluehills Oct 05 '17 at 11:36
@bluehills as I alluded to...I suggest you adapt/correct or try your own newer approach...I find it is the best way to learn MMA and hopefully achieve your goal. – ubpdqn Oct 05 '17 at 11:39

score 0 · Answer 2 · answered Oct 07 '17 at 22:19

You can also use a 2-parameter ParametricPlot3D with options MeshFunctions and Mesh. Using the examples from ubpdqn's answer:

ClearAll[f, g]
f[t_] := 1/2 (3 - 2 E^(-t) + E^t (2 + t))
g[t_] := 1 - 2 E^-t - E^t (2 + t)
a = .5; m = 8;
ParametricPlot3D[{{u, v g[u] + (1 - v) (f[u] + g[u])/2, (1 - v) a},
  {u, (1 - v) f[u] + v (f[u] + g[u])/2, v a}},  {u, 0, 1}, {v, 0, 1}, 
 BoxRatios -> {2, 2, 1}, PlotRange -> {{0, 1}, {-10, 10}, {-1, 1}},
 MeshFunctions -> {# &, #3 &, #5 &, ConditionalExpression[#3, #5 > .5] &}, 
 Mesh -> {m, {a}, {0}, {0.001}}, 
 BoundaryStyle -> Directive[Orange, Dashed], 
 MeshStyle -> {Directive[Orange, Dashed], Directive[Thick, Green], 
   Directive[Thick, Red], Directive[Thick, Blue]}, 
 PlotStyle -> Opacity[.1]]

3D plot of multiple functions

2 Answers2