How to select points from a table that are within some region

Question

there, I encountered this problem while coding:

I generate a table in the r-z plane of cylindrical coordinates:

tbl = Flatten[Table[{r, z}, {r, 0, 1, .1}, {z, -.8, .8, .1}], 1];

and the boundary curve of the region is defined parametrically in the bispherical coordinates:

r[η_, ξ_] := (c Sin[η])/(Cosh[ξ] - Cos[η]);
z[η_, ξ_] := (c Sinh[ξ])/(Cosh[ξ] - Cos[η]);

with the constant:

c = ρ Sin[η0];(*ρ Sin[η0]*)
ρ = (2/(3 (π - η0) Cos[η0] + 3 Sin[η0] - 
  Sin[η0]^3))^(1/3);

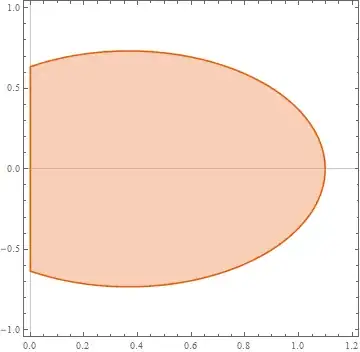
Thus, given the fixed η0, such as η0=π/3, plot the curve:

η0=Pi/3;
ParametricPlot[{r[η0, ξ], z[η0, ξ]}, {ξ, -30, 30}, PlotRange -> All]

I want to select the points that lie inside of the region bounded by the curve and the y-axis, but I don't know how to add this condition to "Select". Please help!

Your curve isn't closed. I assume you want to bound the region with $x>0$ ? — Julien Kluge, Oct 04 '17 at 20:12
yes, sorry, I didn't describe it correctly, I want the points inside of the region bounded by the curve and the y-axis — Ying Zhang, Oct 04 '17 at 20:16
Look up RegionFunction and define your region by statements such as $0<x<1.2$ and $-X(x) < y < + X(x)$, where $X(x)$ is derived from you implicit equations. Once you have a region function you can use RegionMember applied to each point. — David G. Stork, Oct 04 '17 at 20:33
Alternativly to Vitaliy's answer, you could also solve the equation to a $y(x)$ function as mentioned by David with xiSols = Normal[Solve[x == r[\[Eta]0, xi], xi, Reals]] ySol = z[\[Eta]0, xi] /. xiSols // Simplify — Julien Kluge, Oct 04 '17 at 20:37
Welcome to Mathematica.SE! I suggest that: 1) You take the introductory Tour now! 2) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! 3) As you receive help, try to give it too, by answering questions in your area of expertise. — Vitaliy Kaurov, Oct 04 '17 at 21:00

Vitaliy Kaurov · Answer 1 · 2017-10-04T20:36:06.527

8

You should parametrize your region. c looks to me like sort of a radius and it will help to cut off half a plane.

tbl=Flatten[Table[{r,z},{r,0,1,.1},{z,-.8,.8,.1}],1];

r[η_,ξ_, c_]:=(c Sin[η])/(Cosh[ξ]-Cos[η]);
z[η_,ξ_, c_]:=(c Sinh[ξ])/(Cosh[ξ]-Cos[η]);

η0=Pi/3;
ρ=(2/(3 (π-η0) Cos[η0]+3 Sin[η0]-Sin[η0]^3))^(1/3);
c0=ρ Sin[η0];

rig = Region[ParametricRegion[{{r[η0, ξ, c], z[η0, ξ, c]}, 
    0 < c < c0}, {{ξ, -30, 30}, c}], Epilog -> Point[tbl]]

sel=Select[tbl,RegionMember[rig,#]&];

Region[ParametricRegion[{{r[η0,ξ,c],z[η0,ξ,c]},0<c<c0},
{{ξ,-30,30},c}],Epilog->Point[sel]]

I am not sure why some points look they slightly sticking out of the region, - might be drawing imprecision or an issue. You should check this as I am out of time, I hope it's a start.

edited Oct 04 '17 at 20:36

answered Oct 04 '17 at 20:34

Vitaliy Kaurov

73,078
9
204
355

1

beat me by just 1 minute. – Julien Kluge Oct 04 '17 at 20:35
1

@JulienKluge it is always a race here ;-) – Vitaliy Kaurov Oct 04 '17 at 20:37
1

Many appreciations to both of you! – Ying Zhang Oct 04 '17 at 20:38
@Julien Kluge can you please also post your answer if you're not using the same method? – Ying Zhang Oct 04 '17 at 20:38
1

@JulienKluge yes if you are doing something else feel free to post. – Vitaliy Kaurov Oct 04 '17 at 20:39
@VitaliyKaurov I tried to run your code on my computer, but, what is this Region function? What does it do? I can't find it in the Wolfram Documentation, and my current version is 10.4 – Ying Zhang Oct 06 '17 at 13:51
@YingZhang I use 11.2. It just shows a region. Use PlotRegion then. – Vitaliy Kaurov Oct 06 '17 at 17:00
@YingZhang And you can always check online docs: http://reference.wolfram.com/language/ref/Region.html – Vitaliy Kaurov Oct 06 '17 at 17:01
@VitaliyKaurov Oh, got it! Thanks!! – Ying Zhang Oct 07 '17 at 04:08

score 7 · Accepted Answer · answered Oct 04 '17 at 21:12

As suggested i present an alternative solution.

But keep in mind, this depends on the ability to solve your implicit equations and therefore, does not work everytime. But when it works it yields a fast Boolean condition.

We doing the following. Consider your set of equations, depending on the parameter $\xi$.

$$(x,y)=(r(\xi),z(\xi))$$

We solve the first one for the parameter and plug this solution into the other equation. We hope to not only solve this, but to get at least 2 equations which bound your region in $y(x)$.

$$\xi=r^{-1}(x)\\ y(x)=z(r^{-1}(x))$$

We can get the $r^{-1}$ with

xiSols=Normal[Solve[x==r[\[Eta]0,xi],xi,Reals]]

which has two solutions. So we've already won. Plug this into the second equation:

{ySolL,ySolR}=z[\[Eta]0,xi]/.xiSols//Simplify

The sign signals us that ySolL < ySolR and therefore ySolL < y < ySolR

We can easily check this:

RegionPlot[ySolL<=y<=ySolR,{x,0,1.2},{y,-1,1}]

So you could now either:

create a region and check with Element
Use the fast Boolean condition directly ySolL<=y<=ySolR && x > 0

tblIn=Select[tbl,(ySolL<=y<=ySolR&&x>=0)/.{x->#[[1]],y->#[[2]]}&];

With the plot

Show[RegionPlot[ySolL <= y <= ySolR, {x, 0, 1.2}, {y, -1, 1}], ListPlot[tblIn]]

+1. The lack of an upper limit on $x$ becomes a problem if there are points to the right of the region though. — C. E., Oct 04 '17 at 21:34

How to select points from a table that are within some region

2 Answers2

Linked