2

I'm brand new to Mathematica and having to use it for my PDE class. One of my homework questions involves plotting the first few terms of the Fourier series of a solution to a PDE, but the eigenvalues are positive solutions to an equation, for example $tan(p)=p$. How can I get a sequence $p_n$ where $p_n$ is the $n^{th}$ positive solution to the equation?

Zachary F
  • 121
  • 2
  • Welcome to Mathematica.SE! I suggest the following: 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Take the tour! 3) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! – Michael E2 Oct 06 '17 at 18:19
  • Related/duplicate: https://mathematica.stackexchange.com/questions/65896/how-to-find-the-nth-zero-of-a-function – Michael E2 Oct 06 '17 at 19:13

1 Answers1

1

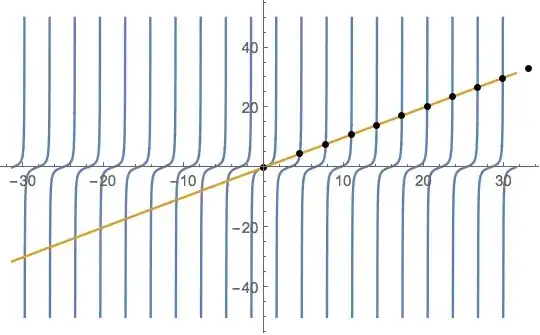
Do you mean something like this?

nmax = 10;
tlist = t /. Table[FindRoot[Tan[t] == t, {t, -0.1 + Pi n}], {n, 0, nmax}];
Show[
 Plot[{Tan[t], t}, {t, -nmax Pi, nmax Pi}, PlotRange -> All],
 ListPlot[{tlist, tlist}\[Transpose], PlotStyle -> Black]
 ]

Otherwise, you should be a bit more specific...

enter image description here

Henrik Schumacher
  • 106,770
  • 7
  • 179
  • 309
  • You can also use Epilog: nmax = 10; tlist = Select[ t /. Table[FindRoot[Tan[t] == t, {t, -0.1 + Pi n}], {n, 0, nmax}], 0 < # < nmax Pi &] Plot[{Tan[t], t}, {t, 0, nmax Pi}, PlotRange -> All, Epilog -> {Red, AbsolutePointSize[4], Point[{#, #} & /@ tlist]}, PlotLegends -> "Expressions"] – Bob Hanlon Oct 06 '17 at 17:30
  • No, I need to be able to evaluate an expression involving the nth solution – Zachary F Oct 06 '17 at 17:31
  • @ZacharyF. tlist is a list, in order, of the roots. That sounds like what you want. – march Oct 06 '17 at 17:35