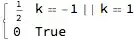If I sum all the positive-numbered Fourier coefficients of $\cos(x)$, I get the correct answer. If I sum the negative-numbered ones, I get a wrong answer. Splitting the sum into two parts somehow fixes the issue.
Sum[FourierCoefficient[Cos[x], x, k], {k, 1, Infinity}]
Sum[FourierCoefficient[Cos[x], x, -k], {k, 1, Infinity}]
Sum[FourierCoefficient[Cos[x], x, -k], {k, 1, 2}] + Sum[FourierCoefficient[Cos[x], x, -k], {k, 3, Infinity}]
Out:
1/2
0
1/2