Can I trust area calculations over discrete MeshRegions? Flipped triangles, possible visual bug

Question

The following code produces a MeshRegion in two different ways. Unfortunately, the first method produces weird artifacts in RegionPlot and Plot3D, whereas the second method causes no such problems. I am hoping to find out if this purely a visual bug or if the mesh is actually corrupted in the first example.

On Mathematica 11.0.1.0 Windows x64 I get the following output:

(* first method *)
<< NDSolve`FEM`
EM1 = ToElementMesh[Circle[], MaxCellMeasure -> Infinity];
MR1 = MeshRegion[EM1];

(* second method *)
MR2 = DiscretizeRegion[Disk[]];

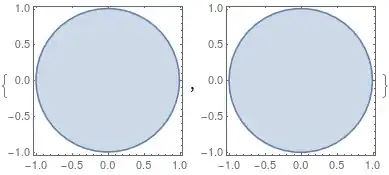
RegionPlot /@ {MR1, MR2}
Plot3D[-Exp[x^2 + y^2], {x, y} \[Element] #] & /@ {MR1, MR2}

I suspect that this is purely a visual bug because the area of MR1 is calculated very precisely: Area[MR1]/Pi returns 0.996981. Also, FindMeshDefects@MR1 returns no defect. I would hope that someone could shed a light on this weird (visual?) bug, as I am working with discrete MeshRegions like the one from the first method and I am not fully sure if I can trust the area calculations any more.

EDIT: The use of RegionPlot applied to Regions is advertised as a new feature in Mathematica 11 here. The conversion between MeshRegion and ElementMesh is discussed in Section "Comparing ElementMesh and MeshRegion" of this tutorial.

EDIT2: I think the documentation of MeshRegion and/or ToElementMesh need to make the differences between inbuilt regions and discretized regions abundantly clear. This tutorial is a good start but the main documentation is lagging behind. There are many undocumented subtleties that you can only learn from other users. For instance:

• As we see in the present question, RegionPlot struggles with MeshRegions of MeshOrder 2, but does OK with an ElementMesh of the same order: RegionPlot /@ {EM1, MeshRegion[EM1]}. I believe the use of RegionPlot@EM1 is undocumented, so is MeshOrderAlteration, I learned it from user21's answer to the present question.
• Boolean operations such as RegionDifference work for inbuilt regions like Disk[], but not for discretized regions. I know this because C.E. told me so in his answer to this question. think it's not obvious from the documentation that inbuilt and discretized regions are not treated on the same footing. To achieve boolean operations of discretized regions, you need workarounds such as the one demonstrated by Henrik Schumacher in this question.

I hope these problems can be addressed in future versions and the documentation can be updated.

Bug reported to Wolfram CASE:3983893.

Answer 1

Here is the correct way to do it:

RegionPlot /@ {EM1, MR2}
Plot3D[-Exp[x^2 + y^2], {x, y} \[Element] #] & /@ {EM1, MR2}

What you are seeing has to do with the fact that ElementMesh use higher order elements (EM1["MeshOrder"]) to approximate the region and functions that take MeshRegion as an argument can not handle that.

To check the area of the ElementMesh use

\[Pi] - Total[EM1["MeshElementMeasure"], 2]
0.009482917945401237`

But here is a much more subtle thing to be aware of. If you use the full dimensional region i.e. Disk (like you did in your DiscretizeRegion example - why the inconsistency?) not Circle you get a much better representation:

EM2 = ToElementMesh[Disk[], MaxCellMeasure -> Infinity];
\[Pi] - Total[EM2["MeshElementMeasure"], 2]
2.2342021526178257`*^-6

It may be possible to improve the Circle case but it's not a high priority.

Another thing you can do is convert the higher order ElementMesh to a first order mesh and then do the conversion like so:

RegionPlot[MeshRegion[MeshOrderAlteration[EM2, 1]]]

Comments

A few things to know: An ElementMesh is not a Region as you can check that with RegionQ. This may change in the future but that's the situation in V11.2. The primary purpose in ElementMesh 's life is to serve as a mesh for the Finite Element Method and have a default mesh order of of 2. As such the ElementMesh is used in NDSolve and related functions such as InterpolatingFunction objects. It can also be used in NIntegrate. I think all of these usages are shown in one of the FEM tutorials. An ElementMesh can be converted to a MeshRegion and the resulting MeshRegion is also second order accurate. This is undocumented MeshRegion functionality but needed to make the geometry frame work to work. A conversion to a second order MeshRegions does not mean, however, that all functions (that allow RegionQ) can deal with that (yet), which is understandable, I think. But does that mean an ElementMesh should also be first order accurate only? Certainly not - that would give lousy FEM results. So what you see here is issues/bugs as the arise at the interface of projects. I filed the plotting over second order mesh regions as a bug; that said I can not say when it's fixed as this is not my department and I have little control over that. The documentation you cite as 'a good start' is one from the FEM framework that I wrote. If you have suggestions for that I am open to changes etc; but I am not going to document short comings of MeshRegion there - it's just not the right place. So my suggestion is that you report MeshRegion issues to wolfram. It does make a difference if issues are reported in house or by customers. Having said that I added an example for MeshOrderAlteration to the ElementMesh generation tutorial, pending approval. The fact that you can plot over ElementMesh is made use of several times in that tutorial - granted it does not show it for every single plot... So, again, if you have anything that is ElementMesh oriented and you'd like to see documented or where the documentation should be improved let me know.