How to plot a list to look like step function?

Question

Suppose I have the following simple list.

l = {0,2,5,9,14};

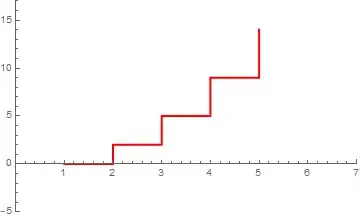
I want to to make a plot that looks like the figure below.

I.e. I want to have a horizontal line between all the numbers in the list that increases by 1 unit in vertical height between the numbers aswell, so it looks more or less like a staircase.

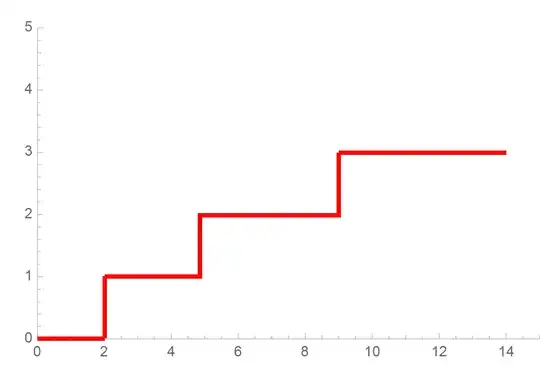
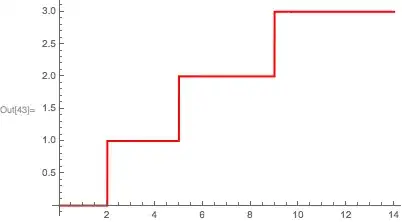
How can I do it? I've tried Discreteplot and kinda works, the only thing is that the axes are inverted and I can't add vertical lines that connects with the horizontal lines like in the figure.

I don't understand why it is so difficult to see that only one of the answers below reproduces the OP's figure. Yet the wrong answers have garnered five upvotes altogether so far. Makes me think this is a deeper question than it first appeared to me. (+1) — Michael E2, Oct 09 '17 at 12:56

Anjan Kumar · Accepted Answer · 2017-10-09T09:23:50.397

16

l = {0, 2, 5, 9, 14};
a0 = Total[UnitStep[t - l]] - 1;
Plot[a0, {t, First[l], Last[l]}, Exclusions -> None, Frame -> True, 
 PlotStyle -> {Directive[Red, Thick]}]

edited Oct 09 '17 at 09:23

answered Oct 09 '17 at 09:18

Anjan Kumar

4,979
1
15
28

I've tried the different solutions given in this thread and this seems like the solution with the least computational time required. – Turbotanten Oct 24 '17 at 07:41

score 9 · Answer 2 · edited Jun 16 '20 at 09:23

9

The simplest way to make it is ListLinePlot with option InterpolationOrder:

l = {0,2,5,9,14};
ListLinePlot[l, InterpolationOrder -> 0, PlotStyle -> Directive[Red, Thick], 
    PlotRange -> {{0, 7}, {-5, 17}}]

The generated plot looks like bellow:

Revision

Thanks @Michael E2 for reminding me. I misunderstand @Turbotanten at first. Bellow is my new revision.

data = Thread[{{0, 2, 5, 9, 14}, Range[0, 4]}];
ListLinePlot[data, InterpolationOrder -> 0, 
    PlotStyle -> Directive[Red, Thick], Frame -> True]

To eliminate the right most vertical line:

ListLinePlot[data /. {x_, y_} /; x == Max[l] -> {x, 3}, InterpolationOrder -> 0, 
    PlotStyle -> Directive[Red, Thick], Frame -> True]

edited Jun 16 '20 at 09:23

Community

1

answered Oct 09 '17 at 10:42

PureLine

1,310
7
20

Why does your domain run from 1 to 5, while the OP's runs from 0 to 14 on the same data? – Michael E2 Oct 09 '17 at 19:20
@MichaelE2 Thanks for reminding. But I could not eliminate the right most vertical line elegantly. – PureLine Oct 10 '17 at 05:19
I suppose one could clip that vertical line with Clip[]: data = Thread[{{0, 2, 5, 9, 14}, Clip[Range[0, 4], {0, 3}]}]... – Michael E2 Oct 10 '17 at 16:39

e.doroskevic · Answer 3 · 2017-10-09T10:11:37.820

8

Also, if you have a version 10.2 or above, you could use ListStepPlot

Module[
 {l},
 l = {0, 2, 5, 9, 14};
 ListStepPlot[l]
 ]

EDIT
Reversing the axis

Module[
 {l},
 l = {0, 2, 5, 9, 14};
 ListStepPlot[l, ScalingFunctions -> {"Reverse", Identity}]
 ]

edited Oct 09 '17 at 10:11

answered Oct 09 '17 at 09:52

e.doroskevic

5,959
1
13
32

1

Yes I actually have version 11.2. Is it possible to invert the axes though? Because I would like to have the unit steps on the vertical y-axis. – Turbotanten Oct 09 '17 at 10:08
1

@Turbotanten see edit above :) – e.doroskevic Oct 09 '17 at 10:11
Why does your domain run from 1 to 6, while the OP's runs from 0 to 14 on the same data? See Carl Woll's answer for a fix. – Michael E2 Oct 09 '17 at 19:19

Carl Woll · Answer 4 · 2017-10-09T15:52:03.193

4

One needs to use the second documented form of ListStepPlot for this:

ListStepPlot[
    Thread[{{0,2,5,9,14},Range[0,4]}],
    PlotRange->{{0,14},{0,5}},
    PlotStyle->Red
]

Update

You could also use StepFunction from my answer to (30055). Here is an example:

sf = StepFunction[Thread[{{0,2,5,9,14},Range[0,4]}], Right];

Plot[sf[t], {t, 0, 14}, PlotStyle->Directive[Thick, Red]]

edited Oct 09 '17 at 15:52

answered Oct 09 '17 at 14:38

Carl Woll

130,679
6
243
355

1

+1. Now there's another correct answer. :) – Michael E2 Oct 09 '17 at 15:55

score 3 · Answer 5 · answered Oct 10 '17 at 03:40

Some other ways. Use Exclusions -> None in the first case to get joined steps.

Plot[Length@l*CDF[EmpiricalDistribution[l], x] - 1, {x, Min@l, Max@l}, PlotStyle -> Red]

Mathematica graphics

Plot[LengthWhile[l, # <= x &], {x, Min@l, Max@l}]
Plot[Count[l, y_ /; y <= x], {x, Min@l, Max@l}]

Mathematica graphics

Less simple, more direct:

xx = l;
yy = Range[0, Length@l - 2];
Graphics[
 {Red, AbsoluteThickness[1.6], 
  Line@ Riffle[{Most@xx, yy}\[Transpose], {Rest@xx, yy}\[Transpose]]},
 Options@ListPlot]

Mathematica graphics

score 2 · Answer 6 · answered Oct 23 '17 at 19:07

2

Here is another way to do it that I came up with

l = {0, 2, 5, 9, 14};
v[x_] := Sum[HeavisideTheta[x - l[[i]]], {i, 1, Length[l]}];
Plot[v[x], {x, 0, Last[l]}, Exclusions -> None, Frame -> True, 
 PlotStyle -> {Directive[Red, Thick]}]

answered Oct 23 '17 at 19:07

Turbotanten

691
5
18

1

In general tho, HeavisideTheta[] is more intended for pure symbolic work rather than numerical evaluation. – J. M.'s missing motivation Oct 24 '17 at 02:21

score 2 · Answer 7 · answered Oct 24 '17 at 02:19

One always has the option of constructing a Piecewise[] function directly:

l = {0, 2, 5, 9, 14};

f[x_] = Piecewise[Transpose[{Range[0, Length[l] - 2],
                             #1 < x <= #2 & @@@ Partition[l, 2, 1]}], Indeterminate]

(This version is right-continuous, but it should not be too hard to modify if you prefer a left-continuous version.)

How to plot a list to look like step function?

7 Answers7

Revision