Impact of Linkage and DistanceFunction on Agglomerate clustering

Question

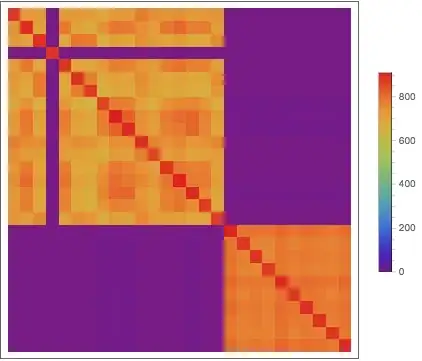
I'm using Agglomerate function to find clusters of my experimental points. I have about 20 points with 10 parameters each. It seems it works fine, but there are plenty of Linkage and DistanceFunction parameters, which impact the final results. The question is .. what does it mean? In which cases clusters should be stable regardless Linkage and DistanceFunction and what its mean if they are different for different Linkage and DistanceFunction? Can I trust such clustering? What are the most "classical" values Linkage and DistanceFunction (default ones?) and why?

Here is my data points:

{{-0.54449, -0.102155, -0.864301, -0.845674, 1.72069,   0.162305, -0.319707, 0.370332, -0.569251, 0.251684}, {-0.823224,   0.466534, -0.275458, -1.13092, -0.630258, -0.421657, -0.25189, -0.764118, 0.0582215,   0.0580152}, {-0.716112, -0.670013, -1.26653, -1.02131, -0.98399, -0.585077, -1.87848, -1.59877, -0.865598, -0.397251}, {-0.615645, -3.06315, 2.06996, -0.918491, 2.83773, 3.6351, 3.05807,   1.20477, -2.63819, -2.88736}, {-0.76705,   0.223083, -0.583763, -1.07343, -0.164866, -0.427301, -0.575523, -0.767708, -0.175055, -0.300879}, {-0.66603, -0.877367, -1.04268, -0.970053, -0.412967, -0.275404, -1.44685, -1.40288, -1.19409, -1.39323}, {-0.754355, -2.75233, -1.70565, -1.06044,   0.52232, -0.0640453, -1.50926, -2.95488, -2.005, -0.977144}, {-0.801445, 0.625306, -0.129547,   0.914166, -0.802012, -0.82025, -0.415802, -0.0372765, 0.310353,   0.203098}, {-1.09105, 0.587188, -0.527171,   0.785344, -0.0154634, -1.69842, -0.703799, -0.993652,   0.317917, -0.182357}, {-0.662017, 0.637865, -0.39368, 1.12361,   0.119336, -0.474191, 0.143626, 0.381655, 0.226684,   0.872835}, {-0.622624, -1.1049, -1.01067, -0.925633, 2.81144,   0.707725, -0.58375, -0.157638, -1.16611, -0.116548}, {-0.795863, -0.405891, -1.3995, -1.10292,   0.996617, -0.0758285, -0.953197, -0.703437, -0.436583,   1.5165}, {-0.850699,   0.422063, -0.0632891, -1.04637, -0.568149, -0.0730285,   0.064865, -0.296008, -0.0367494, 0.353338}, {-0.771168, 0.386542,   0.169187, -1.07765, -0.305672, 0.411273, 0.416447, -0.290914,   0.0557528, -0.0676787}, {-0.729378, 0.625545, -0.292952, 0.716006,   0.114164, -0.156678, 0.266517, 0.315006,   0.268425, -0.188667}, {-0.669941, -0.397554, -0.445959, -0.974056,   0.0886582, 0.543935, 0.116312, 0.0275719, -0.64273,   0.297232}, {-0.589716, -0.661248, -1.12576, -0.891957, -0.11373, -0.0593349, -0.838607, -0.574122, -0.829611, -0.236374}, {1.53941,   0.643217, 1.82853, 1.28692, -0.829425, 1.89118, 1.00785, 1.32393,   1.64218, 3.22573}, {1.2971, 0.576342, 0.217707,   1.10215, -0.329005, -1.22966, 0.323302, 0.398486, 0.427067,   0.091264}, {0.599277, 0.494151, 1.41632, 1.40133, -0.395735,   0.769642, 1.2459, 1.07979, 1.04014, -0.325443}, {1.34088, 0.635507,   0.605183, 1.02062, -0.384553, -0.399112, 0.470923, 0.859018,   0.97534, 0.106176}, {1.41958, 0.64819, 1.00971,   0.784724, -0.807776, -0.586251, -0.331264, 0.338729, 0.885708,   0.464992}, {1.40725, 0.61599, 0.81094,   0.899117, -0.380767, -0.0745943, 0.977698, 0.984784,   0.912223, -0.136263}, {1.12707, 0.56912, 0.461681,   0.611823, -0.751744, -0.556647, -0.141958, 0.485123,   0.811634, -0.447893}, {1.45781, 0.655744, 0.655285,   0.824038, -0.664409, -0.612903, 0.2455, 0.791632, 0.880826,   0.150893}, {1.58214, 0.676405, 1.14394,   0.697673, -0.424202, -0.0852577, 0.750401, 0.949265,   0.975729, -0.000260021}, {0.700286, 0.545816, 0.738454,   0.871389, -0.246233, 0.554472, 0.862678, 1.03132, 0.770765,   0.0655914}}

Answer 1

(Not an answer, but more of an advice how to build confidence in the clustering results.)

For simplicity, I am not using Agglomerate but FindClusters.

Visualization using dimension reduction

Define data with the data given in the question:

data = {{-0.54449, -0.102155, -0.864301,  ...

Find clusters using FindClusters:

cls = FindClusters[data -> Automatic]

(* {{1, 11, 12, 16}, {2, 8, 9, 10, 13, 14, 15}, {3, 5, 6, 
  17}, {4}, {7}, {18}, {19, 20, 21, 22, 23, 24, 25, 26, 27}} *)

In order to visualize the clustering result we reduce the dimension of the data to 3D and plot it. (Rotate interactively the plot in several different directions for better impressions...)

{U, S, V} = SingularValueDecomposition[data, 3];

S

(* {{11.2329, 0., 0.}, {0., 8.8288, 0.}, {0., 0., 4.60382}} *)

pnts = U; (* also try U.S *)

Graphics3D[{PointSize[0.02], 
  MapThread[
   Function[{cl, col}, {col, Point[pnts[[cl]]], 
     Map[Text[#1, pnts[[#1]], {1.5, 1.5}] &, cl]}], {cls, 
    ColorData["DarkRainbow"] /@ Rescale[Range[Length[cls]]]}]}, 
 PlotRange -> All]

In the 3D plot we can see that:

1. the cluster points {19, 20, 21, 22, 23, 24, 25, 26, 27} are indeed clustered closely to each other;

2. the points 4, 7, 18 are indeed separate from the rest;

3. the cluster {1,11,12,16} is somewhat too loose.

It might be because of point 3 different results are obtained with different parameters of Agglomerate.

At this point, though, we can say that by reducing the dimension to 3D and visualizing the result we find the results from FindClusters fairly plausible / making sense.

Multi-dimensional visualization

Alternatively we can visualize the multi-dimensional points in such a way that the clusters examination and evaluation is easier. Here is such visualization using ChernoffFaces.m.

ColumnForm@Block[{rdata = VariablesRescale[data]},
  Map[Function[cl, 
    ChernoffFaceAutoColored[rdata[[#]], ImageSize -> 80, 
       PlotLabel -> #] & /@ cl], cls]
  ]

We can see the similarity of the faces within the clusters and how different are the single cluster points.

Answer 2

In the spirit of Anton's answer, I'd like to present another method that can be used to evaluate clusters. This one works well also for large datasets.

The basic idea is to pick a random sample of a fraction of the data and cluster that. Then repeat this many times and count the number of times that vector $i$ and $j$ ended up in the same cluster. If clusters are well separated then $i$ and $j$ will either always end up in the same cluster, or never end up in the same cluster. If the clusters are not well separated, however, we will see that vectors switch between clusters and this will be easy to spot with a particular visualization that I'll explain below.

Let data be the given data from the question:

data = {{-0.54449, -0.102155, -0.864301,  ...

We now load the HierarchicalClustering package which includes the Agglomerate function and use those functions to implement the algorithm described earlier.

Needs["HierarchicalClustering`"]
consistencyMatrix[data_, nclusters_, niterations_, sampleFraction_: 0.9] := 
 Module[{counts, labeledData, sample, clusters, len},
  len = Length[data];
  counts = SparseArray[{}, {len, len}];
  labeledData = Transpose[{Range@Length@data, data}];

  Do[
   sample = RandomSample[labeledData, Floor[sampleFraction len]];
   clusters = ClusterSplit[ Agglomerate[Last /@ sample -> First /@ sample, Linkage -> "Ward"], nclusters] // Quiet;
   clusters = ReplaceAll[ClusterFlatten /@ clusters, ClusterFlatten[n_] :> {n}];
   Do[counts += SparseArray[Tuples[c, 2] -> 1, {len, len}], {c, clusters}]
   ,
   niterations
   ];
  counts
  ]

We use 1000 random samples and attempt to find, using Agglomerate with the Ward linkage, three clusters. We then plot the matrix given by consistencyMatrix, where element $(i,j)$ counts how many times, out of 1000, the element $i$ ended up in the same cluster as element $j$.

counts = consistencyMatrix[data, 3, 1000];
ArrayPlot[counts, ColorFunction -> "Rainbow", PlotLegends -> Automatic]

This plot tells us a lot already. We can see that there is one vector that always ends up by itself. Out of the 1000 samples, it never appears in a cluster with any other vector. We see two square blocks of vectors which frequently appear in the same clusters as each other, but never in the same cluster as any of the other vectors. In other words, there are at least three well-separated clusters in this dataset given the linkage method and the distance measurement that we use.

We can gain even more information from this visualization, however, if we use agglomerate clustering on the rows to place similar rows next to each other. Let's try it:

reorderConsistencyMatrix[consistencyMatrix_] := Module[{m, newOrder, reordered},
  m = Normal[consistencyMatrix];
  newOrder = ClusterFlatten@Agglomerate[m -> Range@Length@counts] // Quiet;
  reordered = m[[newOrder, newOrder]];
  reordered
  ]

In this code, we didn't look for a specific number of clusters. Agglomerative clustering builds a tree, and we are only interested in how it orders the leaves of the tree because it will put similar vector next to each other.

We now visualize the reordered matrix:

reordered = reorderConsistencyMatrix[counts];
ArrayPlot[reordered, ColorFunction -> "Rainbow", PlotLegends -> Automatic]

This plot is easier to interpret. Now the clusters are side by side, whereas before we found one of the clusters (the single element cluster) inside the block corresponding to another cluster. Furthermore, if we look closely we can see that there are darker orange squares along the diagonal. There, squares represent groups of vectors which are more tightly connected to each other than to the rest of the vectors in that cluster. Counting the number of squares that stand out, if just vaguely, we find that perhaps there may be six clusters and not three. So we try that:

counts = consistencyMatrix[data, 6, 1000];
reordered = reorderConsistencyMatrix[counts];
ArrayPlot[reordered, ColorFunction -> "Rainbow", PlotLegends -> Automatic]

In this plot, we can see, by looking for squares along the diagonal, that we have found six reasonably well-separated clusters. Furthermore, they do not seem to have clusters within the cluster. We can also tell that the second cluster from the left is not as tightly connected as the others, and that cluster three and four from the left are connected to each other to some degree.

What we have done here is to demonstrate that there are six well-separated clusters in this dataset when using the Ward linkage method and the squared Euclidean distance measurement.

To further understand this method, we can also consider the following toy datasets:

Here we have used Agglomerate to find four clusters in uniformly scattered three-dimensional vectors and vectors uniformly distributed within four separated cubic regions. We now apply our method to these datasets:

data2 = RandomReal[1, {1000, 3}];
counts = consistencyMatrix[data2, 10, 20];
reordered = reorderConsistencyMatrix[counts];
ArrayPlot[reordered, ColorFunction -> "Rainbow", PlotLegends -> Automatic]

data3 = Join[
   RandomReal[{0, 0.2}, {250, 3}],
   RandomReal[{0.4, .6}, {250, 3}],
   RandomReal[{0.8, 1}, {250, 3}],
   RandomReal[{1.2, 1.4}, {250, 3}]
   ];
counts = consistencyMatrix[data3, 4, 20];
reordered = reorderConsistencyMatrix[counts];
ArrayPlot[reordered, ColorFunction -> "Rainbow", PlotLegends -> Automatic]

For the uniformly scatter dataset, we looked for ten clusters and didn't find any that are very well separated from all the others. For the other dataset we looked for four clusters, and we found four perfectly separated clusters.