5

I need to find the convex hull for some points in 3D For example: (4,0,0) (2,0,4) (0,1,6) (0,0,10) (0,4,0)

After that I need to see just part of the convex hull which is belong to O(000) part. Also if I can see each part alone.

I hope I explain it well. This is example in 2D In the picture I have the full convex hull Because it is 2D so we can see the convex hull from 4 angels. O(00), O(invinty 0), O(0 invinty) O(invinty invinty) The part of convex hull in O(00) is the one by Red color. The part of convex hull in O(invinty 0) is the one by Green color. The part of convex hull in O(0 invinty) is the one by Blue color. The part of convex hull in O(invinty invinty) is the one by Yellow coclor.

Thank you

enter image description here

george2079
  • 38,913
  • 1
  • 43
  • 110
ateq alsaadi
  • 51
  • 1

2 Answers2

8

I thought this was a nice little puzzle (if I'm understanding it right), but some of the useful information is spread out over the comments. So to clarify, the question is:

Given a set of points in $R^3$, which simplexes of the convex hull can be seen from a given viewpoint?

UPDATE: A (waaay) better function

The function

I realised there's a way to use more natural functions to get this. It's well-hidden, in that Mathematica isn't very good at finding the required region intersections, but there are simple enough ways round that. Anyway, here's the function:

visiblesimplexes2[points_, viewpoint_] := Module[{u, v},
  u = ConvexHullMesh[points];
  v = RegionDifference[ConvexHullMesh[Join[{viewpoint}, points]], u];
  Polygon /@ 
   Intersection[Sort /@ MeshPrimitives[u, 2][[;; , 1]], 
    Sort /@ MeshPrimitives[v, 2][[;; , 1]]]
  ]

The explanation

The idea here (insipired by @george2079's answer) is that if $U$ is the convex hull of points and $V$ is the convex hull of points and viewpoint then $\overline{V\backslash U} \cap U$ will give the points in $U$ that are visible from viewpoint. Getting at this intersection is a little tricky. What I'd like to do would be something simple like RegionIntersection: 

pts = {{4, 0, 0}, {2, 0, 4}, {0, 1, 6}, {0, 0, 10}, {0, 4, 0}};
u = ConvexHullMesh[pts];
v = RegionDifference[ConvexHullMesh[Join[{{0, 0, 0}}, pts]], u];
RegionIntersection[v, u]

(* EmptyRegion[3] *)

The intersection comes up empty, but these regions clearly contain common simplexes, just with their vertices re-ordered:

MeshPrimitives[RegionDifference[v, u], 2][[-3 ;; -1]]
MeshPrimitives[u, 2][[-3 ;; -1]]

(* {Polygon[{{2., 0., 4.}, {0., 1., 6.}, {0., 0., 10.}}], 
    Polygon[{{2., 0., 4.}, {0., 4., 0.}, {0., 1., 6.}}], 
    Polygon[{{2., 0., 4.}, {4., 0., 0.}, {0., 4., 0.}}]}

   {Polygon[{{0., 0., 10.}, {0., 1., 6.}, {2., 0., 4.}}], 
    Polygon[{{0., 1., 6.}, {0., 4., 0.}, {2., 0., 4.}}], 
    Polygon[{{0., 4., 0.}, {4., 0., 0.}, {2., 0., 4.}}]} *)

The workaround is to sort the vertices of each polygon into canonical order so that Mathematica can recognise them as the same. It might be possible to rebuild them into a MeshRegion and get the RegionIntersection that way, but it seemed easier to leave them as a list of vertices, find the list-Intersection, and turn them back into polygons.

Polygon /@ Intersection[Sort /@ MeshPrimitives[u, 2][[;; , 1]], 
  Sort /@ MeshPrimitives[RegionDifference[v, u], 2][[;; , 1]]]

(* {Polygon[{{0., 0., 10.}, {0., 1., 6.}, {2., 0., 4.}}], 
    Polygon[{{0., 1., 6.}, {0., 4., 0.}, {2., 0., 4.}}], 
    Polygon[{{0., 4., 0.}, {2., 0., 4.}, {4., 0., 0.}}]} *)

Which is exactly what visiblesimplexes2 finds.

Comparison

Let's do some time comparisons, just because.

pts = RandomReal[{2, 50}, {100, 3}];
vp = RandomReal[1, 3];
AbsoluteTiming[res1 = visiblesimplexes[pts, vp];]
AbsoluteTiming[res2 = visiblesimplexes2[pts, vp];]

(* Check they're giving the same polygons *)
Sort[Sort /@ res1[[;; , 1]]] == Sort[Sort /@ res2[[;; , 1]]]

(* Visualize *)
chm = ConvexHullMesh[pts];
visibleindex = res2 /. KeyMap[Polygon, First /@
    PositionIndex[Sort /@ MeshPrimitives[chm, 2][[;; , 1]]]];
Show[HighlightMesh[chm, Style[{2, visibleindex}, Red]], 
 Graphics3D[{Thick, Line[{vp, RegionCentroid[#]} & /@ res2], PointSize[Large], Point[vp]}]]

(* {3.10758, Null}
   {0.00872563, Null} 
   True *)

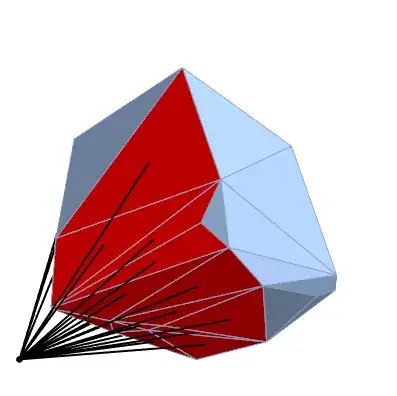
enter image description here

Which is a nice two orders of magnitude improvement.

ORIGINAL POST

TL;DR -- The function

Here's a function that will take your points in the first argument and whatever viewpoint you want in the second, and give you a list of all the polygons of the convex hull that can be seen from that viewpoint. I'll explain it all below.

visiblesimplexes[points_, viewpoint_] := 
 Module[{twosimplexes = MeshPrimitives[ConvexHullMesh[points], 2], intrsct},
  intrsct = With[{line = #}, 
      RegionIntersection[line, #] & /@ 
       twosimplexes] & /@ (Line[{viewpoint, #}] & /@ (RegionCentroid /@
         twosimplexes));
  Pick[twosimplexes, Total /@ (
       (1 - IdentityMatrix[Length[twosimplexes]]) intrsct 
        /. {EmptyRegion[3] -> 0, Point[{x_}] -> 1}
  ), 0]
 ]

Try it on some random data:

pts = RandomReal[{1, 10}, {10, 3}];
vp = RandomReal[1, 3];
visible = visiblesimplexes[pts, vp];
Show[ConvexHullMesh[pts], 
 Graphics3D[{Black, Thick, Line[{vp, RegionCentroid[#]} & /@ visible],
   PointSize[Large], Point[vp], Red, visible}]
 ]

enter image description here

The explanation

First, to set up some basics; define the points, get the convex hull, pull out all the 2-dimensional simplexes, and find their centroids:

pts = {{4, 0, 0}, {2, 0, 4}, {0, 1, 6}, {0, 0, 10}, {0, 4, 0}};
chm = ConvexHullMesh[pts];
twosimplexes = MeshPrimitives[chm, 2];
centroids = RegionCentroid /@ twosimplexes

I'll take the viewpoint here to be the origin {0, 0, 0}, but in the function above it can be any point you want. The idea is to see if a line from the centroid of a simplex to the viewpoint intersects with any other simplexes. If it doesn't, then that simplex is visible from the viewpoint . If it does, then it isn't.

centroidlines = Line[{{0, 0, 0}, #}] & /@ centroids;
intrsct = With[{line = #},
 RegionIntersection[line, #] & /@ twosimplexes] & /@ centroidlines

Intuitively, we'd expect each centroidline to intersect with the simplex it's coming from and, possibly, one or more simplexes that lies between it and the origin. So we just Pick out those simplexes whose centroid lines intersect with only one simplex. Here's a more understandable view of how the intersections work in this example:

MatrixForm[intrsct /. {EmptyRegion[3] -> 0, Point[{x_}] -> x}]

enter image description here

Entry {i, j} in the above matrix denotes the intersection of the line coming from the centroid of the $i^{th}$ simplex with the $j^{th}$ simplex. A 0 indicates that there is no intersection (replacing EmptyRegion[3] for readability). So entries along the diagonal are self-intersections which we're not interested in. Any rows containing off-diagonal entries correspond to centroid lines that intersect other simplexes

To pick out the simplexes with a clear line to the origin, I'm going to set all the diagonals to zero, replace any Points with a 1, and then Total each row. We can then Pick out the simplexes with zero row sums:

selectioncrit = Total /@ (
 (1 - IdentityMatrix[Length[twosimplexes]]) intrsct /. {EmptyRegion[3] -> 0, Point[{x_}] -> 1}
)
visible = Pick[twosimplexes, selectioncrit, 0]
Show[chm, Graphics3D[{Black, Thick, Pick[centroidlines, selectioncrit, 0], 
  PointSize[Large], Point[{0, 0, 0}], Red, visible}]]

(* {Polygon[{{0., 0., 10.}, {0., 1., 6.}, {2., 0., 4.}}], 
    Polygon[{{0., 1., 6.}, {0., 4., 0.}, {2., 0., 4.}}], 
    Polygon[{{0., 4., 0.}, {4., 0., 0.}, {2., 0., 4.}}]} *)

enter image description here

The function above just crams all of that into a couple of (pretty unreadable) lines, and allows the viewpoint to vary.

aardvark2012
  • 5,424
  • 1
  • 11
  • 22
2

Here is a way to do this in 2d. Essentially you complement the convex hull with a new convex hull including the extra point:

SeedRandom[0]
p = RandomReal[{-1, 1}, {10, 2}];
hullpts = ConvexHullMesh[p]["VertexCoordinates"];
hulledges = ConvexHullMesh[p]["Edges"];
pref = {-1., 0.};
g1 = Graphics[{Point@p, {Red, Point[pref]}, 
   Line[hullpts[[#]]] & /@ hulledges}]

enter image description here

compute a new convex hull including the reference point:

new = ConvexHullMesh[Join[hullpts, {pref}]];
Show[{new, g1}]

enter image description here

find vertices on original hull that have been eliminated

dropped = Union@Flatten[Position[hullpts, #] & /@
     Complement[hullpts, new["VertexCoordinates"]]];

find the end points

posref = Position[new["VertexCoordinates"], pref][[1, 1]];
endpoints = 
  Position[hullpts, #][[1, 1]] & /@ (new["VertexCoordinates"][[#]] & /@         
     DeleteCases[Union[Flatten[Select[new["Edges"] ,
         MemberQ[#, posref] &]]] , posref]);
seepoints = Join[ dropped , endpoints ];

find the edges connecting the found points:

seeedges = 
  Select[ hulledges , 
   MemberQ[seepoints, #[[1]]] && MemberQ[seepoints, #[[2]]] & ];
Graphics[{Point@p, {Red, Point[pref]}, 
  Line[hullpts[[#]]] & /@ hulledges,
  {Thick, Red, Line[hullpts[[#]]] & /@ seeedges}}]

enter image description here

the extension to 3d should be straightforward.

george2079
  • 38,913
  • 1
  • 43
  • 110
  • Thank you, I think I did not explain what I want well. In 2D we can see our convex hull from 4 angels of view (each view will be lines) the most important part for me the view from O (0,0) so I just need the part that I colored by Red. In 3D convex hull will consist of triangles connected to each others. I need to see how many triangle can I see from the angle of view O (0,0,0). Colors does not matter. – ateq alsaadi Oct 13 '17 at 17:07
  • I think that's what I did, in the above code pref is your viewpoint. It may simplify things a bit if you restrict the viewpoint to be the corner of the bounding box, but no a lot. – george2079 Oct 13 '17 at 17:48