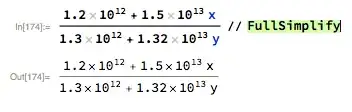How to simplify numbers

Question

Here is an example:

Obviously one could cancel $10^{12}$ from the numerator and denominator. I think Mathematica does not do it because this operation is not exact in floating point arithmetic (these are machine numbers). But I don't really care about that level of precision here. How can I force Mathematica to do the cancellation?

(I cannot do it by hand, because this expression is generated automatically inside a bunch of other functions in my code.)

I know there are other, possibly better duplicates of this question. Please comment if you find one so that I can add it to the header. — Mr.Wizard, Oct 13 '17 at 19:19

score 3 · Answer 1 · answered Oct 13 '17 at 18:45

3

One more way is as follows.

expr = (1.2*10^12 + 1.5*10^13 x)/(1.3*10^12 + 1.32*10^13 y);
Rationalize[expr, 0.01] // Simplify

$$ \frac{6 (25 x+2)}{132 y+13}$$

answered Oct 13 '17 at 18:45

user64494

26,149
4
27
56

3

Rationalize[expr, 0] is arguably safer and it works in this case. – Mr.Wizard Oct 13 '17 at 19:15

kglr · Answer 2 · 2017-10-13T19:15:55.427

1

This works in version 9:

Simplify @ Rationalize @ Factor @ (1.2*10^12 + 1.5*10^13 x)/(1.3*10^12 + 1.32*10^13 y)

(6 (2 + 25 x))/(13 + 132 y)

it doesn't in version 11.

edited Oct 13 '17 at 19:15

answered Oct 13 '17 at 18:56

kglr

394,356
18
477
896

1

This does not work here... see https://imgur.com/a/mJPH9. – a06e Oct 13 '17 at 18:58
@becko, it works in version 9. Just confirmed that it doesn't in version 11. – kglr Oct 13 '17 at 19:15
Any idea why it does not work in v11? Who is the culprit, Factor, Rationalize or Simplify? – a06e Oct 13 '17 at 19:24
1

@becko, Factor[expr] gives the expr back in v11, so it must be the culprit. – kglr Oct 13 '17 at 19:28

score 0 · Answer 3 · answered Oct 13 '17 at 17:57

0

You can try converting these to ints (as the FractionalPart will be zero)

(1.2*^12 + 1.5*^13 x)/(1.3*^12 + 1.3210*^13 y) /. 
  r_Real?(FractionalPart[#] === 0. &) :> IntegerPart[r] // FullSimplify

(60 (2 + 25 x))/(130 + 1321 y)

answered Oct 13 '17 at 17:57

b3m2a1

46,870
3
92
239

How to simplify *numbers*

3 Answers3

How to simplify numbers