I have N points in the from of triplets {xi,yi,zi}.
I would like to bin them on a grid nbin^2 based on their x, y values. Now, the key difference compared to this question is that I would like to compute average values in each bin for binned number of points and obtain {xav,yav,zav} for bin 1, up to nbin^2 and to plot nbin^2 number of points instead of initial N points.
I do not want to plot it against bin values as in example above, and please note that x, y will not be equidistant.
I started the code for pair {xi,yi} and it does what I want (please see below), I am stuck how to effectively extend it in 3D and ideally optimise in line with something like this.
test = RandomInteger[{-100, 100}, {1000, 2}];
xmin = Min@test[[1 ;;]][[All, 1]];
xmax = Max@test[[1 ;;]][[All, 1]];
ymin = Min@test[[1 ;;]][[All, 2]];
ymax = Max@test[[1 ;;]][[All, 2]];
nbin = 15.;
t2 = BinLists[
test[[1 ;; ;; 1]], {xmin, xmax, (xmax - xmin)/nbin}, {ymin,
ymax, (ymax - ymin)/nbin}];
Length /@ {t2, t2[[1]]}
(* getting rid of empty bins*)
ct2 = Replace[t2, x_List :> DeleteCases[x, {}], {0, Infinity}];
ave1 = Map[Mean, ct2[[#]], 1] & /@ Range[Length[ct2]];
ListPlot /@ {test, ave1}
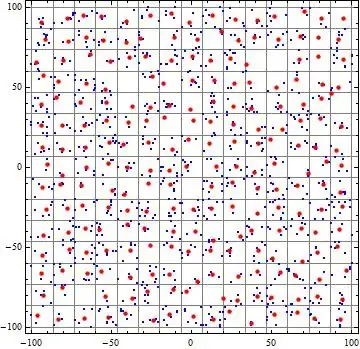
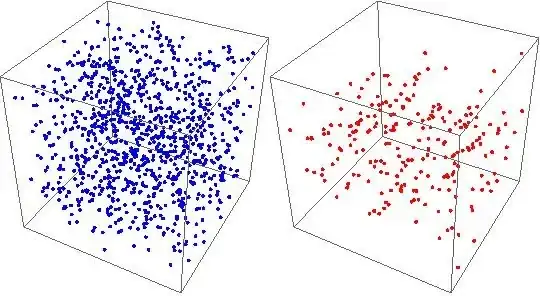
indexeswas wrong, now fixed. – kglr Oct 17 '17 at 00:06nbins^2is for both 2D and 3D. I will post an update with a fix. – kglr Oct 17 '17 at 02:07nbin^2grid for both 2D and 3D input. – kglr Oct 17 '17 at 04:37