ListPointPlot3d to visualize points close to a manifold

Question

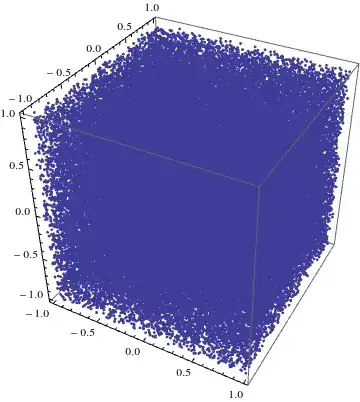
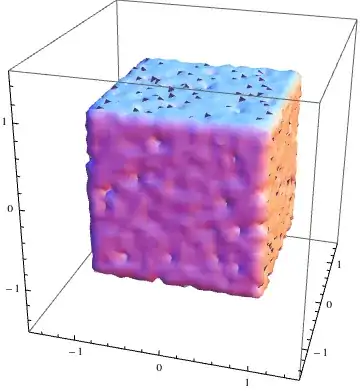
I have a large set of points that are close to manifold which I want to show in a ListPointPlot3D. Using part of the data set illustrates this

plot http://vollmer.ms/homog3d_0

plot http://vollmer.ms/homog3d_1

there are fewer data points in the middle.

But using all the data with

ListPointPlot3D[list[[2 ;; n]]]

results in

plot http://vollmer.ms/homog3d_2

Is there a better way to visualize this? Somehow something like 3d contour plot of the density.

Although the title doesn't mention it, this seems to be about fitting a surface to a point list. If so, it's a possible duplicate of Construct a simple mesh or tetrahedral mesh from 3D image surface — Jens, Dec 05 '12 at 23:28
A theme that generally needs this kind of computation is the SPH computational fluid dynamics method, where a "continuous" mass of water is processed as a very big set of "drops" of water. At the end, to render it, you need algorithms to regroup then into a surface. Since this method is also used on game development, you should be able to find a lot of algorithms (not on Mathematica...) by searching by that theme. — P. Fonseca, Dec 06 '12 at 07:37

score 3 · Accepted Answer · answered Dec 05 '12 at 23:46

3

If your point cloud is extremely "thick" you can create a RegionFunction. Here is a simple example using points in the cube from -1 to 1 in all directions.

pts = RandomReal[{-1, 1}, {10^5, 3}];

ListPointPlot3D[pts, BoxRatios -> 1]

enter image description here

Now create the function.

nf = Nearest[pts];

inRegion[pt : {_Real, _Real, _Real}, eps_Real] := 
 TrueQ[Norm[nf[pt, 1][[1]] - pt] < eps]

This will give an approximation to the boundary enclosing the region. We decide a point is "in" if it is within .04 of one of the points in the original list, else it is outside.

d = 1.5;
reg = RegionPlot3D[
  inRegion[{x, y, z}, .04], {x, -d, d}, {y, -d, d}, {z, -d, d}, 
  Mesh -> False, PlotPoints -> 40]

enter image description here

This code was gleefully cribbed from some work here (Also here)

answered Dec 05 '12 at 23:46

Daniel Lichtblau

58,970
2
101
199

Thank you very much for the help. The problem with this approach is that I have outliers, and they get a ball around them, too. I am trying to use the cluster function, but this does not seem to work. – warsaga Dec 06 '12 at 00:31
Try it with Norm[nf[pt, 2][[2]] - pt]; that should force there to be at least two nearby points in order to be considered "inside". – Daniel Lichtblau Dec 06 '12 at 00:33
that is good but terribly slow.. – warsaga Dec 08 '12 at 17:01
I'm mildly surprised about the speed issue. Can you give details on how to produce a data set typical of the sort you encounter? – Daniel Lichtblau Dec 08 '12 at 20:54

score 1 · Answer 2 · answered Dec 06 '12 at 04:40

In addition to what @Daniel Lichtblau described, let me give you a further idea. It is not completely clear whether it really helps in your case since frome the statement

I have a large set of points that are close to manifold

I can only guess and an example data-set would have been better.

What I would try is to estimate the local density of points and to make a ContourPlot3D (or a RegionPlot3D) which shows you the boundary of certain density.

You could for instance (and this is the difference to Daniels approach) calculate the distances from a point x to the next, say 30 points and then calculate the Mean or Median distance. This gives you kind of an estimation how dense x is surrounded by points.

Example:

data = ExampleData[{"Geometry3D", "StanfordBunny"}, "VertexData"];
With[{nf = Nearest[data]},
 density[x : {__?NumericQ}] := Mean[Map[Norm[x - #] &, nf[x, 30]]]
 ];
RegionPlot3D[
 density[{x, y, z}] < .01, {x, -.15, .1}, {y, -.1, .1}, {z, 0, .2}, 
 BoxRatios -> Automatic, PlotPoints -> 40]

Mathematica graphics

I like that. Could be useful in situations where sample points are relatively sparse. What I did kinda falls flat in such areas. (Plus 1, as they say. Whoever "they" is.) — Daniel Lichtblau, Dec 06 '12 at 14:48
@DanielLichtblau Thanks but it's stolen or at least inspired by the Kernel density estimation. — halirutan, Dec 06 '12 at 17:18

ListPointPlot3d to visualize points close to a manifold

2 Answers2