Michaelis–Menten kinetics using Gillespie Algorithm

Question

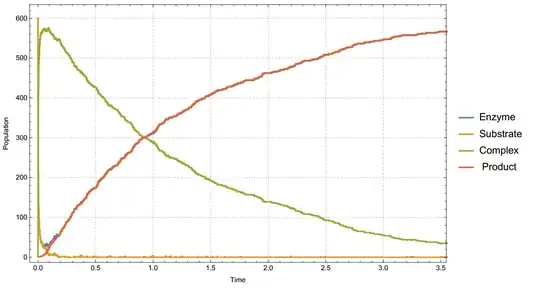
I am trying to implement Michaelis–Menten kinetics using Gillespie Algorithm.

$$\text{Reaction 1:}\quad E+S\rightarrow C$$

$$\text{Reaction 2:}\quad C\rightarrow E+S$$ $$\text{Reaction 1:}\quad C\rightarrow E+P$$

Each reaction has a rate with a weight

$$\text{Reaction rate 1:}\quad k_1 ES$$

$$\text{Reaction rate 2:}\quad k_2 C$$ $$\text{Reaction rate 3:}\quad k_3C$$

and time is distributed exponentially. $$t\sim Exp(rate)$$

Minimun t means that reaction occures.

It kinda works for two reactions. How can I modify the code for 3 or more reactions. I have seen this code but I would like to learn coding and algorithm.

{k1 = 1.1, k2 = 0.1, k3 = 0.8, e = 100, s = 100, c = 1, p = 1, 
  numOfReaction = 100, numOfsim = 10};

sim = NestList[(
     Δt1 = 
      RandomVariate@ExponentialDistribution[k1  #[[2]] #[[3]]];
     Δt2 = 
      RandomVariate@ExponentialDistribution[k2  #[[4]]];
     Δt = Min[Δt1, Δt2];
     If[Δt1 < Δt2, {#[[
         1]] + Δt, #[[2]] - 1, #[[3]] - 1, #[[4]] + 
        1}, {#[[1]] + Δt, #[[4]] - 1, #[[2]] + 
        1, #[[3]] + 1}]) &, {0, e, s, c}, numOfReaction];

ListStepPlot[{Transpose@{sim[[All, 1]], sim[[All, 2]]}, 
  Transpose@{sim[[All, 1]], sim[[All, 4]]}}, 
 PlotLegends -> {"Simulation"}, 
 PlotStyle -> Directive[AbsoluteThickness[0.2]], Frame -> True, 
 PlotTheme -> "Detailed", FrameLabel -> {"Time", "Population"}, 
 ImageSize -> Large]

I have tried this code but it does not work.

NestList[(
   Δt1 = 
    RandomVariate[ExponentialDistribution[k1  #[[2]] #[[3]]]];
   Δt2 = 
    RandomVariate[ExponentialDistribution[k2  #[[4]]]];
   Δt3 = 
    RandomVariate[ExponentialDistribution[k3  #[[4]]]];
   Δt = 
    Min[{Δt1, Δt2, Δt3}];
   If[Δt1 < Δt2, {#[[
       1]] + Δt, #[[2]] - 1, #[[3]] - 1, #[[4]] + 
      1}, {#[[4]] - 1, #[[2]] + 1, #[[3]] + 1}];
   If[Δt1 < Δt3, {#[[
       1]] + Δt, #[[2]] - 1, #[[3]] - 1, #[[4]] + 
      1}, {#[[4]] - 1, #[[2]] + 1, #[[5]] + 1}];
   If[Δt2 < Δt3, {#[[
       1]] + Δt, #[[4]] - 1, #[[2]] + 1, #[[3]] + 
      1}, {#[[4]] - 1, #[[2]] + 1, #[[4]] + 1}]) &, {0, e, s, 
  c}, numOfReaction]

Taking a guess, maybe the three reaction case needs to determine which delta_t was minimal, rather than have three if's? Alternatively, maybe each should be used, with the changes from the later ones dependent on values updated from earlier ones. — Daniel Lichtblau, Oct 21 '17 at 16:04

OkkesDulgerci · Answer 1 · 2017-10-29T13:49:24.560

Here it is the improved version. It works now. But there is an issue.

I would like to run #[[4]] > 0 but substrate reach 0 earlier than complex and ExpDist[0] gives error. What I want is #[[3]] =1 if #[[3]] =0. Basically, I would like to keep #[[3]] =1 not 0 so that iteration does not stop and stop only #[[4]] >0

With[{k1 = 1.1, k2 = 0.1, k3 = 0.8, e = 100, s = 100, c = 1, p = 1},
 sim = NestWhileList[(
    time = {RandomVariate@ExponentialDistribution[k1  #[[2]] #[[3]]], 
      RandomVariate@ExponentialDistribution[k2  #[[4]]], 
      RandomVariate@ExponentialDistribution[k3  #[[4]]]};
    \[CapitalDelta]t = Min[time];

          f[x_] := 
           Piecewise[{{{#[[1]] + \[CapitalDelta]t, #[[2]] - 1, #[[3]] - 
                1, #[[4]] + 1, #[[5]]}, 
              x == 1}, {{#[[1]] + \[CapitalDelta]t, #[[2]] + 1, #[[3]] + 
                1, #[[4]] - 1, #[[5]]}, 
              x == 2}, {{#[[1]] + \[CapitalDelta]t, #[[2]] + 1, #[[
                3]], #[[4]] - 1, #[[5]] + 1}, x == 3}}];reaction = Ordering[time, 1][[1]];
     f[reaction]) &, {0, e, s, c, p}, #[[3]] > 0 &]];
{t, e, s, c, p} = Transpose@sim;

    ListStepPlot[{Transpose@{t, e}, Transpose@{t, s}, Transpose@{t, c}, 
      Transpose@{t, p}}, Frame -> True, PlotTheme -> "Detailed", 
     FrameLabel -> {"Time", "Population"}, ImageSize -> Large, 
     PlotLegends -> {"Enzyme", "Substrate", "Complex", " Product"}]

I would like to run #[[4]] > 0 but substrate reach 0 earlier than complex and ExpDist[0] gives error. What I want is #[[3]] =1 if #[[3]] =0. Basically, I would like to keep #[[3]] =1 not 0 so that iteration does not stop and stop only #[[4]] >0. How can I do it? — OkkesDulgerci, Nov 09 '17 at 18:22

OkkesDulgerci · Accepted Answer · 2017-12-27T19:12:15.260

Here is a different approach.

With[{k1 = 1.1, k2 = 0.1, k3 = 0.8, e = 1000, s = 1000, c = 1, p = 1},
   sim = NestWhileList[(
      a1 = k1 #[[2]] #[[3]] ;
      a2 = k2 #[[4]];
      a3 = k3 #[[4]];
      a0 = Total@{a1, a2, a3};
      reaction = 1/a0 Accumulate@{a1, a2, a3};

      pos = First@FirstPosition[reaction, _?(# > RandomReal[] &)];
      \[CapitalDelta]t = 1/a0 Log[1/RandomReal[]];

      Which[ 
       pos == 
        1, {#[[1]] + \[CapitalDelta]t, #[[2]] - 1, #[[3]] - 
         1, #[[4]] + 1, #[[5]]},
       pos == 
        2, {#[[1]] + \[CapitalDelta]t, #[[2]] + 1, #[[3]] + 
         1, #[[4]] - 1, #[[5]]},
       pos == 
        3, {#[[1]] + \[CapitalDelta]t, #[[2]] + 1, #[[3]], #[[4]] - 
         1, #[[5]] + 1}]

      ) &, {0, e, s, c, p}, #[[4]] > 0 &]];
{t, e, s, c, p} = Transpose@sim;

    ListStepPlot[{Transpose@{t, e}, Transpose@{t, s}, Transpose@{t, c}, 
      Transpose@{t, p}}, Frame -> True, PlotTheme -> "Detailed", 
     FrameLabel -> {"Time", "Population"}, ImageSize -> Large, 
     PlotLegends -> {"Enzyme", "Substrate", "Complex", " Product"}, 
     PlotStyle -> {Thick}]

How can I use stopping criteria like so (#[[3]]>0&&#[[4]] > 0) & Meaning that I would like to iteration stop when both substrate and complex are 0 — OkkesDulgerci, Oct 25 '17 at 02:54

Michaelis–Menten kinetics using Gillespie Algorithm

2 Answers2

Linked