How can I show the extremum clearly in Plot3D?

Question

 p11[x_, δ_, b11_] := 1/x^4 + (2 b11)/x^2 + 4/x - 4 b11 x - 
  1/(1 + (-1 + x^3) (1 + δ)^3)^(4/3) - (
  2 b11)/(1 + (-1 + x^3) (1 + δ)^3)^(2/3) - 
  4/(1 + (-1 + x^3) (1 + δ)^3)^(1/3) + 
  4 b11 (1 + (-1 + x^3) (1 + δ)^3)^(1/3)
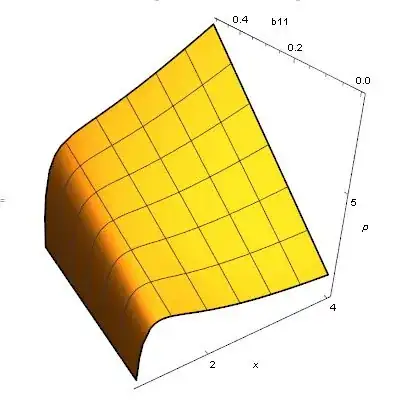
Plot3D[p11[x, 0.01, b11]/0.01, {x, 1, 4}, {b11, 0, 0.5}, 
 Boxed -> False, AxesLabel -> {x, b11, p}, Mesh -> 5, 
 PlotLegends -> Automatic, BoundaryStyle -> Thick, AxesStyle -> Black,
  ViewPoint -> {-1.2, -2, 1.5}, 
 Ticks -> {{0, 2, 4}, Automatic, {5, 10}}, BoxRatios -> {1, 1, 1}]

Q:I want to show the maximum(or the peak) in red color, and the minmum(or the Valley) in blue.

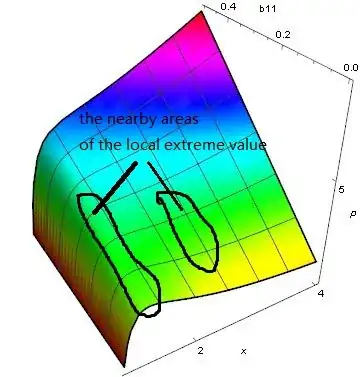
color the local maximum region and the local minimum region

I want to see the location of the vally in colors, and how it changes with b11. I wonder if ColorFunction can do this? Can MMA color the nearby area of local extreme value in different color with others?

just like this

The extremum can be found like this Abs[D[p11[x, 0.01, b11], x]]=0.

You could use something like Show[(* plot *), Graphics3D[{{Red, Sphere[(* max location *), 0.02]}, {Blue, Sphere[(* min location *), 0.02]}}]]. — J. M.'s missing motivation, Oct 25 '17 at 08:41
Thank you for your suggestion! But I want to know how the function p[]-x change with b11 from 3Dplot, not the number solutions. — keanhy, Oct 25 '17 at 09:23
Now what you sought, but I prefer: ColorFunction -> "Rainbow". — David G. Stork, Oct 25 '17 at 15:19
Related question: https://mathematica.stackexchange.com/q/94595 — m_goldberg, Oct 25 '17 at 16:27

score 3 · Answer 1 · answered Oct 25 '17 at 15:10

3

p3d = Plot3D[p11[x, 0.01, b11]/0.01, {x, 1, 4}, {b11, 0, 0.5}, 
     Boxed -> False, AxesLabel -> {x, b11, p}, Mesh -> 5, 
     PlotLegends -> Automatic, BoundaryStyle -> Thick, 
     AxesStyle -> Black, ViewPoint -> {-1.2, -2, 1.5}, 
     Ticks -> {{0, 2, 4}, Automatic, {5, 10}}, BoxRatios -> {1, 1, 1}];

{min, max} = #[p3d[[1, 1]], Last] & /@ {MinimalBy, MaximalBy};
Show[p3d, Graphics3D[{PointSize[.05], Blue, Point@ First @ min, Red, Point@ First @ max}]]

answered Oct 25 '17 at 15:10

kglr

394,356
18
477
896

Better to use Sphere than Point in 3D don't you think? – m_goldberg Oct 25 '17 at 16:23
@m_goldberg, I agree; but plain Sphere gives ellipsoids, and felt lazy to find the right values for the second argument:) – kglr Oct 25 '17 at 16:31
In such cases I use Ellipsoid to adjust the markers to spherical. – m_goldberg Oct 25 '17 at 16:36
Sorry about my bad description, I just redescribe the question. Can MMA color the nearby area of local extreme value in different color just like the third picture? – keanhy Oct 26 '17 at 01:48

m_goldberg · Answer 2 · 2017-10-26T02:48:02.950

The plot really looks better with spheres marking the extrema. And since kglr doesn't want to take the time to write the code to make such markers, I will will supply it.

p11[x_, δ_, b11_] := 
  1/x^4 + (2 b11)/x^2 + 4/x - 4 b11 x - 1/(1 + (-1 + x^3) (1 + δ)^3)^(4/3) - 
  (2 b11)/(1 + (-1 + x^3) (1 + δ)^3)^(2/3) - 4/(1 + (-1 + x^3) (1 + δ)^3)^(1/3) + 
  4 b11 (1 + (-1 + x^3) (1 + δ)^3)^(1/3)

surface = 
  Plot3D[p11[x, 0.01, b11]/0.01, {x, 1, 4}, {b11, 0, 0.5},
    Boxed -> False, AxesLabel -> {x, b11, p}, Mesh -> 5, 
    PlotLegends -> Automatic, BoundaryStyle -> Thick, 
    AxesStyle -> Black, ViewPoint -> {-1.2, -2, 1.5}, 
    Ticks -> {{0, 2, 4}, Automatic, {5, 10}}, BoxRatios -> {1, 1, 1}]

{min, max} = 
  Chop[#[surface[[1, 1]], Last] & /@ {MinimalBy, MaximalBy}, 10^-5][[All, 1]]

extrema =
  With[{r = .03 (max - min)}, 
    Graphics3D[{Blue, Ellipsoid[min, r], Red, Ellipsoid[max, r]}]];

Show[surface, extrema, PlotRange -> All]

r is computed from the formula

 r = scaleFactor {xRange, yRange, zRange} = scaleFactor (max - min)

where scalarFactor is picked by eye.

How can I show the extremum clearly in Plot3D?

2 Answers2