Using brackets with limits in evaluation of definite integral

Question

How to do this in Mathematica: $$\int_1^2 x^2 \, dx=\left[\frac{x^3}{3}\right]_1^2$$ or $$\int_1^2 x^2 \, dx=\left.\frac{x^3}{3}\right|_1^2$$ Also is there a function that represents the right hand side?

Answer 1

I would do it the easy way, I would use MaTeX. :)

Here is an automated function. Here is an improved version which uses aligned which makes the output more clear, Kept old version at bottom

ClearAll[x]
Needs["MaTeX`"]
SetOptions[MaTeX,"Preamble"->{"\\usepackage{amssymb,amsmath,latexsym,amsfonts,amsthm}"}];

toX[any_]:=ToString@TeXForm@any

doInt[f_,x_,from_,to_]:=Module[{int,low,up},int=Integrate[f,x];
  up=Limit[int,x->to];
  low=Limit[int,x->from];
  MaTeX["
\\begin{aligned}
\\int_"<>toX[from]<>"^"<>toX[to]<>" "<>toX[f]<>" \\, dx &= "<>toX@int<>"\\bigg|_"<>toX[from]<>"^"<>toX[to]<>"\\\\
&= \\left["<>toX@int<>"\\right]^"<>toX[to]<>" - \\left["<>toX@int<>"\\right]^"<>toX[from]<>"\\\\ 
&= "<>"\\left("<>toX@up<>"\\right)-\\left("<>toX@low<>"\\right)\\\\ 
&= "<>toX[Simplify[up-low]]<>"
\\end{aligned}",
Magnification->3]
]

To use

doInt[x^2, x, 1, 2]

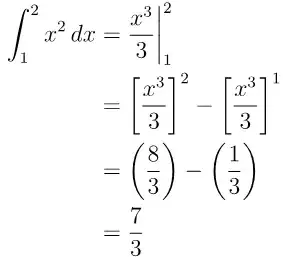
Old answer

ClearAll[x]
<< MaTeX`
toX[any_] := ToString@TeXForm@ any
doInt[f_, x_, from_, to_] := Module[{int, low, up},
  int = Integrate[f, x];
  up = Limit[int, x -> to];
  low = Limit[int, x -> from];
  MaTeX["\\int_" <> toX[from] <> "^" <> toX[to] <> " " <> toX[f] <> 
    " \\, dx = "
    <> toX@ int <> "\\bigg|_" <> toX[from] <> "^" <> toX[to] <>
    " = \\left[" <> toX@ int <> "\\right]^" <> toX[to] <> 
    " - \\left[" <> toX@ int <> "\\right]^" <> toX[from] <> " = " <>
    "\\left(" <> toX@up <> "\\right)-\\left(" <> toX@low <> 
    "\\right) = " <> toX[Simplify[up - low]], Magnification -> 3]
  ]

Now just do

doInt[x^2, x, 1, 2]

doInt[Sin[x]*x,x,0,Pi]

doInt[Exp[x]+3 Sin[x],x,0,Pi]

Answer 2

Maybe this helps, but I think it is a bit elaborated:

HoldForm[Integrate[x^2, {x, 1, 2}]] == 
 RowBox[{"", Integrate[x^2, x], 
  SubsuperscriptBox[StyleBox["\[VerticalSeparator]", 30], 
  AdjustmentBox["1", BoxBaselineShift -> 2], 
  AdjustmentBox["2", BoxBaselineShift -> -2]]}] 
 //DisplayForm // TraditionalForm

You could be interested in this solution.

Answer 3

Here is an implementation of a function EvaluatedAt that attempts to answer your question. The DownValues are easy:

EvaluatedAt[func_, x_, low_, high_] := ReplaceAll[func, x->high] - ReplaceAll[func, x->low]
EvaluatedAt[func_, x_, pt_] := func /. x->pt

The tricky part is how to make use of and format the unevaluated version of EvaluatedAt. I like the Inactive/Activate approach for these kinds of things instead of HoldForm/ReleaseHold. So, I will introduce an Inactive format for EvaluatedAt.

To do this I will make use of my function Initial from my answer to How can one manually change the rule ordering, which I provide below:

Initial /: Verbatim[TagSetDelayed][Initial[sym_], lhs_, rhs_] := With[
    {
    new = Block[{sym},
        TagSetDelayed[sym, lhs, rhs];
        First @ Language`ExtendedDefinition[sym]
    ],
    protect = Unprotect[sym]
    },

    sym;
    Quiet @ MakeBoxes[sym[], TraditionalForm];
    Unprotect[sym];

    Replace[new,
        Rule[values_, n:Except[{}]] :> (
            values[sym] = DeleteDuplicates@Join[n, values[sym]]
        ),
        {2}
    ];
    Protect@protect;
]

Using Initial, we can create a FormatValues for Inactive[EvaluatedAt][..] (unfortunately, EvaluatedAt is buried too deep to attach the format to it):

Initial[Inactive] /: MakeBoxes[Inactive[EvaluatedAt][f_, x_, low_, high_], form_] := 
TemplateBox[
    {MakeBoxes[f, form], MakeBoxes[x, form], MakeBoxes[low, form], MakeBoxes[high, form]},
    "InactiveEvaluatedAt",
    DisplayFunction -> (
        SubsuperscriptBox[
            RowBox[{#1, StyleBox["\[RightBracketingBar]", "Inactive", FontFamily->"Times"]}],
            #3,
            #4
        ]&
    ),
    InterpretationFunction -> (
        RowBox[{
            RowBox[{"Inactive", "[", "EvaluatedAt", "]"}], 
            "[",
            RowBox[{#, ",", #2, ",", #3, ",", #4}],
            "]"
        }]&
    )
]

Initial[Inactive] /: MakeBoxes[Inactive[EvaluatedAt][f_, x_, at_], form_] := 
TemplateBox[
    {MakeBoxes[f, form], MakeBoxes[x, form], MakeBoxes[at, form]},
    "InactiveEvaluatedAt",
    DisplayFunction -> (
        SubscriptBox[
            RowBox[{#1, StyleBox["\[RightBracketingBar]", "Inactive", FontFamily->"Times"]}],
            #3
        ]&
    ),
    InterpretationFunction -> (
        RowBox[{
            RowBox[{"Inactive", "[", "EvaluatedAt", "]"}],
            "[",
            RowBox[{#, ",", #2, ",", #3}],
            "]"
        }]&
    )
]

It's a bit complicated because I want the output to be able to be copy/pasted/evaluated. A few comments. I used a SubscriptBox/SubsuperscriptBox around the expression so that the vertical bar can grow as the expression gets taller. I used "\[RightBracketingBar]" instead of "|" for the bar because of spacing. Finally, I used the "Times" font for the bar because I don't want the little bump that the StandardForm font gives the bar. I think the rest of the code is pretty standard for Inactive formatting.

It should be straightforward to modify it to use [..] instead of ..| if you so desire.

Now, for your example:

Inactive[Integrate][x^2, {x, 1, 2}] == Inactive[EvaluatedAt][x^3/3, x, 1, 2]
Inactive[Integrate][x^2, {x, 1, 2}] == Inactive[EvaluatedAt][x^3/3, x, 1, 2] //TraditionalForm

Activate@%

True

One final comment. Mathematica has the character "\[LeftAutoMatch]" which should be equivalent to TeX's "\left.". It didn't seem to be needed, so I didn't use it, but it's possible that it should be added.

Answer 4

Based on Josè's nice answer, I would define my own function:

 fun [f_, g_, h_ ] :=  
 DisplayForm[ 
  RowBox[{"", f, 
    SubsuperscriptBox[StyleBox["\[VerticalSeparator]", 30], 
     AdjustmentBox[g, BoxBaselineShift -> 2], 
     AdjustmentBox[h, BoxBaselineShift -> -2]]}]  ]  

so you can use it to show the rhs for different operations and different upper and lower limits without changing the definition.

for example try fun[D[x^2, x ], 2, 4]