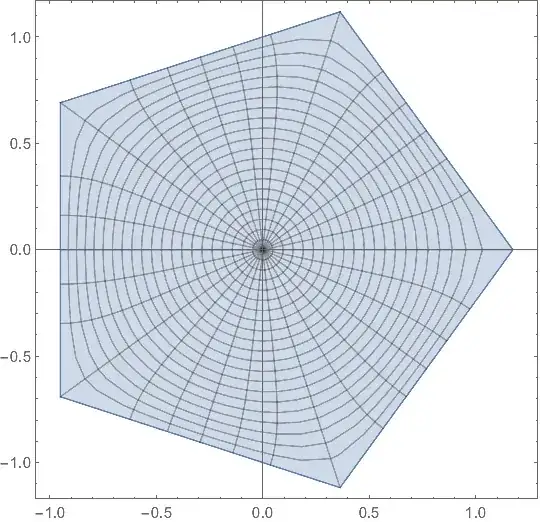
The function $$F(z)=\int_0^{z}(1-\zeta^n)^{-\frac{2}{n}}d\zeta$$ maps the open unit disk $\Bbb{D}=\{z\in\Bbb{C} : |z|\lt 1\}$ conformally on to the interior of a regular polygon with $n$ sides.
How can I visualize the images of circles $C_r=\{re^{i\theta} : 0\le\theta\le 2\pi\}$ with $0\lt r\lt 1$ under $F$ ?
I have never use Mathematica to do something like this. So I appreciate any thing that you can do related to this.
Asked
Active
Viewed 1,324 times
5
Bumblebee
- 359
- 3
- 10
-
1Take a look at this https://mathematica.stackexchange.com/questions/15637/plotting-complex-numbers-as-an-argand-diagram/15643#15643 – Artes Nov 01 '17 at 18:55
-
@Artes: I looked at the linked question and tried to work along those answer, but could not succeed. Everything I tried runs long time and give back some error. – Bumblebee Nov 02 '17 at 01:16
-
1See this as well. – J. M.'s missing motivation Nov 02 '17 at 03:09
1 Answers
9
Here is a working example. We set up a the function F (only a rather coarse numerical approximation to the integral is used). Afterwards, we plot it with ParametricPlot. The function ReIm converts complex numbers to 2-dimensional vectors; otherwise, ParametricPlot won't plot anything.
n = 5;
F[z_?NumericQ] := ReIm[NIntegrate[Power[(1. - (t z)^n), -2/n] z, {t, 0, 1}, AccuracyGoal -> 4]]
ParametricPlot[
F[r Exp[I s]], {s, -Pi, Pi}, {r, 0., 1.},
Mesh -> {6 n - 1, 20},
PlotPoints -> {6 n - 1, 20},
MaxRecursion -> 1
]
Edit: As Carl Woll pointed out, the can obtain the integral symbolically. So let's generated a more accurate version of F. (Warning: This will take a while.)
Block[{z, n},
F = {z, n} \[Function]
Evaluate[Integrate[Power[(1 - (t z)^n), -2/n] z, {t, 0, 1},
Assumptions -> n > 0] /. ConditionalExpression[a_, b___] :> a
]
];
The advantage is that the drawing is now much quicker.
n = 7;
m = 6;
ParametricPlot[ReIm[F[r Exp[I s], n]], {s, -Pi, Pi}, {r, 0, 1},
Mesh -> {m n - 1, 20},
PlotPoints -> {m n + 1, 20},
MaxRecursion -> 2
]
Henrik Schumacher
- 106,770
- 7
- 179
- 309
-
A couple suggestions. 1. You can symbolically integrate to obtain
t Hypergeometric2F1[1/n,2/n,1+1/n,t^n]2. I would use the equivalentParametricPlot[F[r Exp[I s]], ..]instead. – Carl Woll Nov 01 '17 at 23:00 -
Ah, the symbolic computation finally finishes! I did not expect that! – Henrik Schumacher Nov 01 '17 at 23:12
-
Thank you very much for your detailed and helpful answer. I appreciate it very much. These days I am studying Schwarz-Christoffel mappings and these transformations are bit difficult understand as they re given by integrals. For example map from the unit dist to interior of a Pentagram has the form $$\int_0^z\dfrac{(1-z^5)^{2/5}}{(1+z^5)^{4/5}}dz.$$ Therefore I am curious that; Is there any way that we can do this visualization with the integral representation of a function $F$ ? – Bumblebee Nov 02 '17 at 00:35
-
@Bumblebee, you can, but it's going to be slow since you need to integrate a function with singularities over the complex domain. But, since your particular example has a nice closed form, it would be a shame not to use it:
With[{n = 15}, ParametricPlot[With[{z = r Exp[I s]}, ReIm[z AppellF1[1/5, -2/5, 4/5, 6/5, z^5, -z^5]]], {s, -Pi, Pi}, {r, 0., 1.}, Mesh -> {10 n - 1, 20}, PlotPoints -> {10 n - 1, 20}, MaxRecursion -> 1]]– J. M.'s missing motivation Nov 02 '17 at 03:10