Consider a model where the nonlinearity is in $x'(t)$ and not in the highest derivative $x''(t)$.
eq1 = {x''[t] + Sin[ x'[t]] + x[t] == u[t]};
Choose the first state as $x(t)$ (call it $\bar{x}_1(t)$) and the second state as $x'(t)$ (call it $\bar{x}_2(t)$) and we get the following equations.
$$ \bar{x}_1'(t)=\bar{x}_2(t)$$
$$ \bar{x}_2'(t)+\sin \left(\bar{x}_2(t)\right)+\bar{x}_1(t)=u(t) $$
And this is exactly what NonlinearStateSpace model does. It does not throw out anything when converting it to a state-space representation.
nssm1 = NonlinearStateSpaceModel[eq1, x[t], u[t], x[t], t]
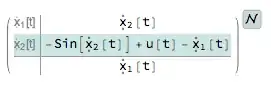
Therefore the simulations match.
OutputResponse[nssm1, UnitStep[t], {t, 0, 5}];
NDSolve[Join[eq1 /. u[t] -> UnitStep[t], {x[0] == 0, x'[0] == 0}], x[t], {t, 0, 5}];
p1 = Plot[Evaluate@Join[%, %%], {t, 0, 5}]

Now consider another model which has the nonlinearity in the highest-order derivative $x''(t)$.
eq2 = {Sin[x''[t]] + Sin[ x'[t]] + x[t] == u[t]};
Then the second state-equation becomes
$$ \sin\left(\bar{x}_2'(t)\right)+\sin \left(\bar{x}_2(t)\right)+\bar{x}_1(t)=u(t) $$
This cannot be represented using NonlinearStateSpaceModel, which requires that the state derivatives all be linear. Thus it will return the same model as before after linearizing the nonlinearity.
nssm2 = NonlinearStateSpaceModel[eq2, x[t], u[t], x[t], t]

And, just to verify, the simulation matches the previous one.
OutputResponse[nssm2, UnitStep[t], {t, 0, 5}];
Show[p1, Plot[%, {t, 0, 5}]]
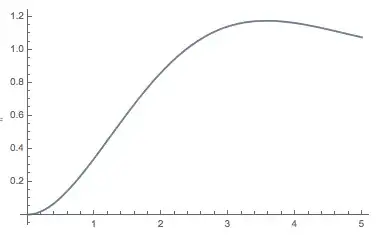
The complete nonlinear model is a different animal.
NDSolve[Join[eq2 /. u[t] -> UnitStep[t], {x[0] == 0, x'[0] == 0}], x[t], {t, 0, 5}]

Update:
As zxczd mentions in the comments to this answer, the complete nonlinear model has multiple solutions. It's interesting to see that model linearized by NonlinearStateSpaceModel approximates just one of them.
{x''[t] == (x''[t] /. Solve[eq2, x''[t]][[1]]) /. C[1] -> 0};
NDSolveValue[{% /. u[t] -> UnitStep[t], {x[0] == 0, x'[0] == 0}}, x, {t, 0, 5}];
Show[ListLinePlot[%, PlotStyle -> Dashed], p1, PlotRange -> {{0, 5}, All}]
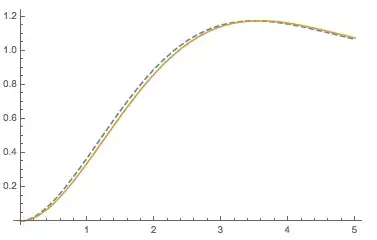
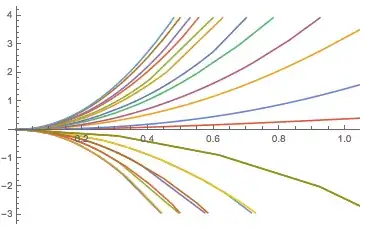
A bigger sample of possible solutions:
possibleeq = Thread[x''[t] == Re[x''[t] /. Solve[eq2, x''[t]] /. C[1] -> #]] & /@
Range[-5, 5] // Flatten;
possiblesol = NDSolveValue[{# /. u[t] ->(*Sin@t*)1, {x[0] == 0, x'[0] == 0}},
x, {t, 0, 5}] & /@ possibleeq;
ListLinePlot[possiblesol]
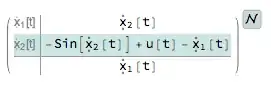








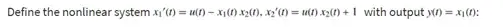 when I typed it by hand for
when I typed it by hand for
SolvedDelayed->TruetoNDSolve. – xzczd Nov 06 '17 at 15:17NDSolvewill be able to solve the problem with a DAE solver. You may want to read this: https://mathematica.stackexchange.com/a/158519/1871 – xzczd Nov 06 '17 at 15:33SolvedDelayedhas been deprecated in my version."EquationSimplification" -> "Residual"works in that it returns the solution 1. – Suba Thomas Nov 06 '17 at 15:45SolveDelayedis red in the notebook, but it just works well, and in certain case you can even circumvent bug with it. (See remark 1 here: https://mathematica.stackexchange.com/a/133140/1871) – xzczd Nov 06 '17 at 15:54SolveDelayedonly find one by default. The following is a way to find more solutions:possibleeq = Thread[x''[t] == Re[x''[t] /. Solve[eq2, x''[t]] /. C[1] -> #]] & /@ Range[-5, 5] // Flatten; possiblesol = NDSolveValue[{# /. u[t] ->(*Sin@t*)1, {x[0] == 1, x'[0] == 0}}, x, {t, 0, 5}] & /@ possibleeq; ListLinePlot[possiblesol]– xzczd Nov 06 '17 at 16:18x2'to giveNonlinearStateSpaceModel[{{x2, ArcSin[-Sin[x2] + u - x1]}}, {x1, x2}, {u}], which yields the (or a) correct result. – CarbonFlambe Nov 07 '17 at 00:33