7

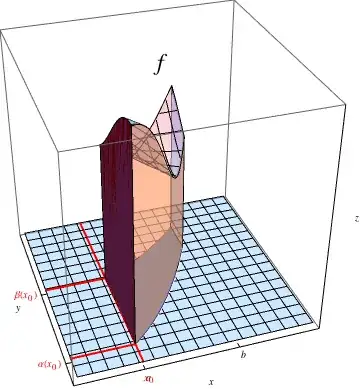
I ran across a wonderful animation on Wikipedia that gave a perfect geometric interpretation about the process of multiple integration (in this case, double integrals). Therefore, I am wondering if something similar can be done in Mathematica, and if it can also be extended to triple integrals. If anyone could also provide the code, I would be very grateful.

This goes way beyond my skill level in Mathematica, therefore I would not even know where to start.

animation

UPDATE

I found this that combined with the animation of the area sheets ($0$ to $ g(x,y)$), running from $x=a$ to $x=b$ and $y=f(a)$ to $y=f(b)$, could create the above animation. I think the hard part (at least for me) would be to create the animation of these sheets and synchronizing the movement with the segments in the x and y axis.

I found out that the above animation was created with Mathematica 9

C. E.
  • 70,533
  • 6
  • 140
  • 264
DMH16
  • 379
  • 2
  • 14
  • Well, it has the distinct look of a 3D plot made by Mathematica, so I'm confident that 'something similar can be done in Mathematica'. As for triple integrals, 4D plots can not be made in Mathematica or with any other plotting software that I'm aware of :-) – m_goldberg Nov 08 '17 at 05:22
  • @m_goldberg oh ok! Thanks. For triple integrals I refer to when the integrand is 1, therefore it should be possible – DMH16 Nov 08 '17 at 06:14

1 Answers1

15

I'll let somebody else do the lines and labels...

slices

f[x_, y_] := Sin[3 x + Sin[3 y]]

reg = BoundaryDiscretizeRegion[ImplicitRegion[x^2 <= y <= x^2/2 + 1,
                                              {{x, 0, 1}, {y, 0, 3/2}}]];
rmf = RegionMember[reg];

plane = Plot3D[-1, {x, -1/2, 2}, {y, -1/2, 2}, 
               ColorFunction -> (If[rmf[{#1, #2}], Blue, White] &), 
               ColorFunctionScaling -> False, Lighting -> "Classic", 
               PlotPoints -> 125];
int = Plot3D[f[x, y], {x, y} ∈ reg, PlotTheme -> "Classic"];

slices = SortBy[Cases[Normal[Plot3D[f[x, y], {x, y} ∈ reg, BoundaryStyle -> None, 
                                    Mesh -> {Subdivide[20]}, MeshFunctions -> {#1 &}, 
                                    PlotStyle -> None]], 
                      Line[l_] :> 
                      Polygon[Join[l, PadRight[Drop[l[[{-1, 1}]], None, -1],
                                               {2, 3}, -1]]], ∞], #[[1, 1, 1]] &];

fr = Table[Show[plane, int, Graphics3D[s], PlotRange -> All, 
           ViewPoint -> {-1.3, -2.4, 1.}], {s, slices}];

ListAnimate[fr]
J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574