Performing geometric transforms on 3D text inside a Graphics3D expression

Question

I am trying to put some 3D text inside a 3D graphics. So far I find two ways to make 3D text.

halirutan in "Rotating an image along a Möbius strip?")

wordData = ImportString[ExportString["Mathematica", "PDF"], "PDF"][[1, 1, 2, 1, 1, 2]];
Graphics3D[Tube[#, 0.2] & /@ Map[Append[#, 0] &, wordData, {2}]]

J.M. in "Strategies for creating 3D text"

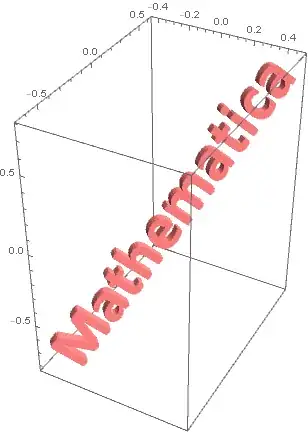
RegionProduct[DiscretizeGraphics[Text[Style["Mathematica", Bold, FontFamily -> "Times"]],
         _Text, MaxCellMeasure -> 0.1], MeshRegion[{{0}, {2}}, Line[{1, 2}]]]

halirutan's method gives a set of coordinates which is easy to manipulate (for example - change position, orientation, colour etc.)

word1=ImportString[ExportString["Hello","PDF"],"PDF"][[1,1,2,1,1,2]];
(*scale=0.5; rotation Pi/4 around {0,1,1}*)
wline1=Map[RotationTransform[Pi/4,{0,1,1}][0.5Join[#,{0}]]&,word1,{2}];

word2=ImportString[ExportString["World","PDF"],"PDF"][[1,1,2,1,1,2]];
(*scale=0.2; shift {1,0,-1}*)
wline2=Map[(0.2Join[#,{0}]+{1,0,-1})&,word2,{2}];

Graphics3D[{Green, Sphere[],
   Blue, Map[Tube[#, 0.3] &, wline1], Red, Map[Tube[#, 0.3] &, wline2]}]

How can I do the same thing with J.M.'s method?

@andre, Thanks, I was not familiar with this option. So I can control the position and orientation with TranslationTransform and RotationTransform. Now I am left with size and colour. I am playing with RegionResize, but can't fix it properly. Should I modify my question with this information or would you like to post a compact answer? — Sumit, Nov 10 '17 at 17:50
Note that the accepted solution is not viable in v11.3 due to a bug. — bobthechemist, Jul 20 '18 at 00:05

score 3 · Answer 1 · answered Nov 10 '17 at 18:10

3

region1=RegionProduct[
   DiscretizeGraphics[Text[Style["Hel", Bold, FontFamily -> "Times"]],
         _Text, MaxCellMeasure -> 0.1], MeshRegion[{{0}, {2}}, Line[{1, 2}]]];

region2=RegionProduct[
   DiscretizeGraphics[Text[Style["lo", Bold, FontFamily -> "Times"]],
         _Text, MaxCellMeasure -> 0.1], MeshRegion[{{0}, {2}}, Line[{1, 2}]]];

region2Rotated=TransformedRegion[region2,RotationTransform[Pi/2, {1, 0, 0}]];  

region2RotatedTranslated=TransformedRegion[region2Rotated,TranslationTransform[ {12, 0, 3}]];  

RegionPlot3D[{region1,region2RotatedTranslated}]

I seem to recall that in a video, Stephen Wolfram himself says that TranslationTransform directly applied to a Region should work.
Maybe soon...

answered Nov 10 '17 at 18:10

andre314

18,474
1
36
69

Great! The last line gives RegionPlot3D::argr: RegionPlot3D called with 1 argument; 4 arguments are expected. (MMA11.1). RegionPlot3D[region1] is working fine. Would you like to comment on the controlling the size? – Sumit Nov 10 '17 at 18:33
I don't have the error message "1 argument.." neither on 11.0 nor on 11.2 (I don't have 11.1) – andre314 Nov 10 '17 at 18:38
Concerning "size controlling", I don't see very well what you mean and I'm not a expert. You can ask the question in the chat. I will see if I know something interesting. – andre314 Nov 10 '17 at 18:40
I modified my question to clarify what I am looking for. At the end, I have to combine different object with Graphics3D like Show[Graphics3D[Sphere[]], RegionPlot3D[region1], RegionPlot3D[region2]] – Sumit Nov 11 '17 at 08:52

score 3 · Accepted Answer · answered Nov 11 '17 at 09:44

Alternatively, extract the points and Polygon[]s with MeshCoordinates[] and MeshCells[], and then apply any transformation function to the points before passing to GraphicsComplex[], like so:

message = RegionProduct[DiscretizeGraphics[Text[Style["Mathematica", Bold,
                                                      FontFamily -> "Calibri"]],
                                           _Text, MaxCellMeasure -> 0.1],
                        MeshRegion[{{0}, {2}}, Line[{1, 2}]]];

sc = Max[Abs[Flatten[RegionBounds[message]]]];
pts = Composition[ScalingTransform[{1, 1, 1}/sc], RotationTransform[π/2, {1, 0, 0}]] @ 
      MeshCoordinates[message];
polys = MeshCells[message, 2];

Graphics3D[GraphicsComplex[AffineTransform[RollPitchYawMatrix[{π/3, -π/4, π/6}]][pts],
                           {Directive[EdgeForm[], Pink], polys}], Axes -> True]

rotated text

Just what I am looking for - raw data :) – Sumit Nov 11 '17 at 13:10 — Sumit, Nov 11 '17 at 13:10

Performing geometric transforms on 3D text inside a Graphics3D expression

2 Answers2