How to build and manipulate 2 surface in one box, so that intersection is highlighted and unwanted parts are removed during movement?

Question

As the title indicates, I want to build (and manipulate) two three-dimensional surfaces in one bounding box, so that their intersection is highlighted and the unwanted parts of the surfaces are removed during their movement relative to each other.

First of all I created surface $x=0$ using ContourPlot3D. Here is the corresponding code (I used the right tool?):

cp1 = ContourPlot3D[x == 0, {x, -5, 5}, {y, -5, 5}, {z, -5, 5},
                    AxesLabel -> {"x", "y", "z"}]

which produces this output:

plane

Then I created surface $\cos (x) \sin (y)$ using Plot3D. Here is the corresponding code (I used the right tool?):

Plot3D[Cos[x]*Sin[y], {x, -5, 5}, {y, -5, 5}, AxesLabel -> {"x", "y", "z"}]

which produces this output:

surface

Then I created two three-dimensional surfaces ($\cos (x) \sin (y)$ and $x=0$) in one bounding box. Here is the corresponding code (I used the right tool?):

Show[cp1, Plot3D[Cos[x]*Sin[y], {x, -5, 5}, {y, -5, 5}, AxesLabel -> {"x", "y", "z"}]]

I get this output:

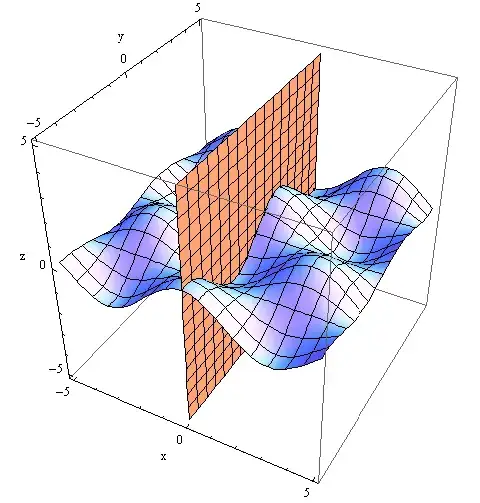
plane and surface

My question is the following: How can I move (manipulate) the surface $x=0$ along the $x$ axis (no movement along the $y$ and $z$ axes), so that surface $x=0$ would be cutoff surface for surface $\cos (x) \sin (y)$ and their intersection is highlighted. Surface $\cos (x) \sin (y)$ not moving.

If for example (this picture is taken not from Mathematics):

example

EDIT

@JM code is not working:

J. M.'s code

The code works in version 10 and 11. If you're using a version older than that, please edit your question to mention the version you are using. — J. M.'s missing motivation, Nov 11 '17 at 01:06
@JM - I have the program "Mathematica 9" on my computer . Can I also put "Mathematica 11" on my computer? Can the two versions stand on the same computer? — sasvak, Nov 12 '17 at 14:23
@JM - I have 11.2 - it's working! I delete my 9 version , because Mathematica installer tell me about it! — sasvak, Nov 12 '17 at 17:35
sasvak, actually, it's possible to have more than one version of Mathematica on a computer. I personally do so to track changes between versions. — J. M.'s missing motivation, Nov 12 '17 at 22:47

J. M.'s missing motivation · Answer 1 · 2017-11-12T23:21:52.960

4

Here's a starting point:

n = 31;
Animate[Show[Plot3D[Cos[x] Sin[y], {x, -5, 5}, {y, -5, 5}, 
                    AxesLabel -> {"x", "y", "z"}, BoundaryStyle -> None, 
                    BoxRatios -> Automatic, Mesh -> {{xx}}, MeshFunctions -> {#1 &}, 
                    MeshStyle -> Directive[Red, Thick], PlotPoints -> 45, 
                    PlotRange -> {-5, 5}], 
             Graphics3D[InfinitePlane[{xx, 0, 0}, Rest[IdentityMatrix[3]]]]],
        {xx, -5, 5, 10/(n - 1)}]

slicing plane

For those working in older versions without InfinitePlane[], use the following instead:

Polygon[{Scaled[{0, 1, 1}, {xx, 0, 0}], Scaled[{0, -1, 1}, {xx, 0, 0}],
         Scaled[{0, -1, -1}, {xx, 0, 0}], Scaled[{0, 1, -1}, {xx, 0, 0}]}]

The technique is quite similar to what I used here.

edited Nov 12 '17 at 23:21

answered Nov 10 '17 at 16:49

J. M.'s missing motivation

124,525
11
401
574

@JM Hello! First of all thank you very much! But my Mathematica give me sign ------ orange "+" in right side -------- Message ---- "InfinitePlane is not a Graphics3D primitive or directive". – sasvak Nov 10 '17 at 17:44
@JM And also surface $x=0$ not drawing, only intersection line is highlighted and moving – sasvak Nov 10 '17 at 17:46
@JM Also moving sometimes hangs (or freeze) link – sasvak Nov 10 '17 at 17:56
How did you save the animation? – Raffaele Nov 11 '17 at 13:24
@Raffaele. what I actually do for exporting an animation is to use, well, Export[] + Table[]: Export["filename.gif", Table[(* stuff *)]] – J. M.'s missing motivation Nov 11 '17 at 13:48
@Raffaele. Right click on picture and choose save graphics as, then choose gif file type – sasvak Nov 12 '17 at 14:31

score 1 · Answer 2 · answered Nov 11 '17 at 16:13

1

Another way with interactivity, and animation:

Manipulate[
Show[
{
Plot3D[{Exp[- 0.09 (x^2 + y^2)] Cos[2 x] Sin[y]}, {x, -5, 5}, {y, -5, 5}, AxesLabel -> {"x", "y", "z"}, 
BoundaryStyle -> None, Mesh -> {{x0}}, 
MeshFunctions -> {#1 &}, 
MeshStyle -> Directive[Black, Thickness[0.01]], 
PlotRange -> {-1, 1}, 
PlotStyle -> {If[u, Opacity[0.8], Opacity[0]]}, 
PerformanceGoal -> "Quality", PlotTheme -> "Business"],

 Graphics3D[{EdgeForm[None], Yellow, 
 If[v, Directive[Opacity[0.8]], Directive[Opacity[0]]], 
 InfinitePlane[{x0, 0, 0}, {{0, 1, 0}, {0, 0, 1}}]}]
}, BoxRatios -> {1, 1, .9}
],
{{x0, -1.5}, -5, 5, 0.1, Appearance -> "Labeled"},
Delimiter,
{{u, True, "f[x]"}, {True, False}}, {{v, True, "Cut plane"}, {True, 
False}},
ControlPlacement -> Top
]

answered Nov 11 '17 at 16:13

José Antonio Díaz Navas

6,103
1
20
30

The code works in version 9? – sasvak Nov 12 '17 at 15:12
@sasvak Sorry, I do not know. Just check it ! Anyway, it is possible that some functions regarding the appearance of the plot will belong to later updates if so, or substitute them with their equivalent. My suggestion is to eliminate them. If some important functions do not work, the code definitely is not for ver 9. Please, when ask a question, indicate the target version of MMA. – José Antonio Díaz Navas Nov 12 '17 at 16:13
@JADN I have 11.2 - it's working! – sasvak Nov 12 '17 at 17:33

How to build and manipulate 2 surface in one box, so that intersection is highlighted and unwanted parts are removed during movement?

2 Answers2