Finding the minima and the transition state in a potential energy surface (PES)

Question

Problem Background:

I am trying to simulate a potential energy surface (PES) which represents the different states that a triatomic molecule (A-B-C) can have in 3D and its corresponding ContourPlot.

The potential function, depending on the distance between atom A and atom B (which I called r) and the distance between atom B an atom C (which I called d) has the following form (which I arbitrarily chose):

crazypotential =  1/r^12 - 2/r^6 + 1/d^12 - 2/d^6 -
(2 Exp[-(r - d)] + 2Exp[-(d - r)] -  2 Exp[-(2 (r - d) - (d - r))*Cos[d]]);

Plot3D[crazypotential, {r, .8, 1.6}, {d, .8, 1.6}]

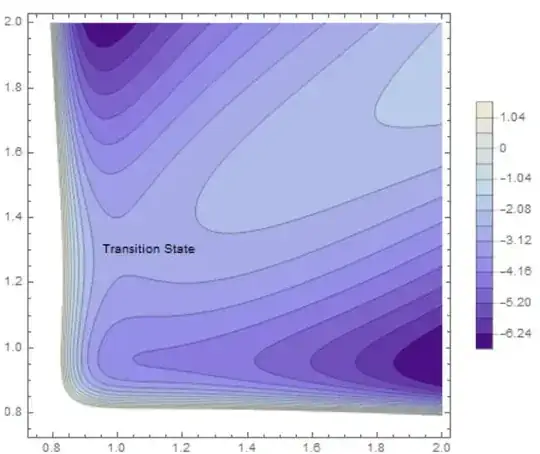
Show[ContourPlot[crazypotential, {r, 0.75, 2}, {d, 0.75, 2}, PlotLegends -> Automatic,
                 Contours -> 15, ContourStyle -> Directive[Black, Opacity[.3]],
                 ColorFunction -> "LakeColors"],
     Graphics[Text["Transition State", {1.1, 1.3}]]]

As you can see, there are clearly two minima and one transition state. Now, my question is the following:

I want to know exactly where the minima (deep blue) and the transition state are. For that I do something like:

Solve[D[crazypotential, {r, d}] == 0 && r < 1.6 && d < 1.6, {r, d}, Reals]

But does not seem to work. Do you have any ideas about how I could try to solve these minima and transition state in this region (both r and d going from 0.8 to 1.6)? Or do you see any mistake in my code that could be the reason why it is not working?

Thank you very much in advance!

Henrik Schumacher · Accepted Answer · 2017-11-10T19:15:54.710

As you know, what you call "transition state" is in particular a critical point of crazypotential, i.e., a point where both partial derivative of crazypotential with respect to r and d vanish. A "root" of the derivative of crazypotential so to say.

You already read off a good guess for the transition state. You can refine that with Newton's method which is effectively performed by FindRoot.

Dcrazypotential = D[crazypotential, {{r, d}, 1}];
FindRoot[Dcrazypotential == {0, 0}, Transpose@{{r, d}, {1.1, 1.3}}]

{r -> 1.01146, d -> 1.31042}

The same is also applicable to the minimizers; they are also roots of Dcrazypotential -- if they exist. I have to say that crayzpotential is not bounded from below on $\mathbb{R}^2$, so there are no global minimizers. Still, there might exist local minimizers...

If you want to constrain r and d to lie between 0.8 and 1.8, then minimimal values are attained at the box boundary. The can be detected with

FindRoot[Dcrazypotential[[1]] == 0 /. d -> 1.8, {r, 1.}]
FindRoot[Dcrazypotential[[2]] == 0 /. r -> 1.8, {d, 1.}]

score 3 · Answer 2 · answered Nov 11 '17 at 01:50

Adapting the approach from this answer, here is how to use the MeshFunctions option of ContourPlot[] to find critical points:

potential[r_, d_] := 1/r^12 - 2/r^6 + 1/d^12 - 2/d^6 -
         (2 Exp[-(r - d)] + 2 Exp[-(d - r)] - 2 Exp[-(2 (r - d) - (d - r)) Cos[d]])

(* gradient and Hessian *)
{dr[r_, d_], dd[r_, d_]} = D[potential[r, d], {{r, d}}];
hes[r_, d_] = D[potential[r, d], {{r, d}, 2}];

crit = Cases[Normal[ContourPlot[dr[r, d] == 0, {r, 3/4, 2}, {d, 3/4, 2}, 
                                ContourStyle -> None, Mesh -> {{0}}, 
                                MeshFunctions -> Function[{r, d, f}, dd[r, d]]]], 
             Point[{r0_, d0_}] :> ({\[FormalR], \[FormalD]} /. 
                                   FindRoot[{dr[\[FormalR], \[FormalD]],
                                             dd[\[FormalR], \[FormalD]]},
                                            {{\[FormalR], r0}, {\[FormalD], d0}}]), ∞]
   {{1.01146, 1.31042}}

where we see that only one critical point is returned. Let's test it:

hc = hes @@ crit[[1]];
Through[{PositiveDefiniteMatrixQ, IndefiniteMatrixQ, NegativeDefiniteMatrixQ}[hc]]
   {False, True, False}

This verifies that the point we found is a saddle point.

Finding the minima and the transition state in a potential energy surface (PES)

2 Answers2