3

I have a numerical solution and I want to find the maximum value of the solution.

a = Rationalize[0.33390683175743086];
b = -0.15;
d = 5;
a1 = 
  u[y_] := 
    (Tanh[a*(y - d)] + Tanh[a*d])/(1 + Tanh[a*d]) + 
      b*Sqrt[3]*y/d*Exp[-1.5*(y/d)^2 + 0.5];
α = 0.04;
ω = Rationalize[0.0060230765816024628] + Rationalize[0.0097304407482613764]*I;
sol = 
  NDSolve[
    {(u[y] - ω/α)*(ϕ''[y] - α^2*ϕ[y]) - u''[y]*ϕ[y] == 0, 
     ϕ[80] == 1, ϕ'[80] == -I*α}, ϕ, {y, 0, 80}][[1, 1, 2]]
ϕ[y_] := sol[y]

So ϕ is the solution of my problem. I difined a new function called uu which is the negative of the derivative of ϕ:

uu[y_] := -ϕ'[y];

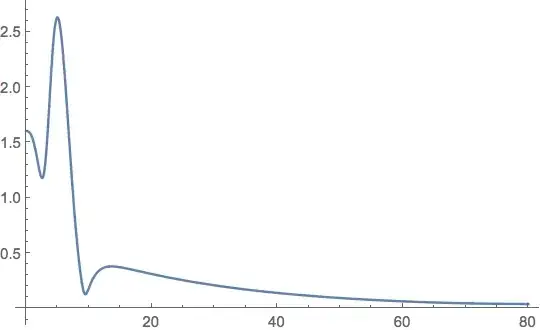
When I plot Abs[uu[y]] I have this:

enter image description here

Now the question is how to determine the maximum value of |uu|? Looking the figure it seems that the value is around for |uu| = 2.6.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Mateus
  • 1,243
  • 7
  • 14

4 Answers4

7

You need to use arbitrary precision rather than machine precision in NDSolve by setting the WorkingPrecision. This then requires that all numeric values have at least that precision. Consequently, Rationalize or set to exact numbers all of your constants. To Rationalize long decimals you need to use a smaller tolerance. 0 will always work. 

a = Rationalize[0.33390683175743086, 0];
b = -3/20;
d = 5;
a1 = u[y_] := (Tanh[a*(y - d)] + Tanh[a*d])/(1 + Tanh[a*d]) + 
    b*Sqrt[3]*y/d*Exp[-3/2*(y/d)^2 + 1/2];
α = 1/25;
ω = Rationalize[0.0060230765816024628 + 0.0097304407482613764*I, 0];

Clear[ϕ];

sol = NDSolve[{(u[y] - ω/α)*(ϕ''[
           y] - α^2*ϕ[y]) - u''[y]*ϕ[y] == 0, ϕ[80] == 
      1, ϕ'[80] == -I*α}, ϕ, {y, 0, 80}, 
    WorkingPrecision -> 15][[1, 1, 2]];

ϕ[y_] := sol[y]

uu[y_] := -ϕ'[y]

Plot[Abs[uu[y]], {y, 0, 80}, PlotRange -> All]

enter image description here

Maximize[{Abs[uu[y]], 0 < y < 80}, y]

(* {2.63046649575507, {y -> 5.00764789850856}} *)

EDIT: Alternatively, rather than setting the WorkingPrecision in NDSolve; instead of using Maximize use NMaximize and set its WorkingPrecision.

NMaximize[{Abs[uu[y]], 0 < y < 80}, y, WorkingPrecision -> 15]

(* {2.63046694880644, {y -> 5.00764953131638}} *)

There is a slight difference in the result.

Also note that just setting the WorkingPrecision in Maximize does not work.

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
  • 1
    Thanks @BobHanlon. Solved. If you could explain me: Why I need to use arbitrary precision rather than machine precision in NDSolve? – Mateus Nov 10 '17 at 20:41
  • 2
    Remove the option for WorkingPrecision and reevaluate; you will get an error message: "NMaximize::cvmit: Failed to converge to the requested accuracy or precision within 100 iterations." Such problems are frequently due to loss of precision using machine precision. Arbitrary precision tracks and controls precision during calculations. The trade-off is that arbitrary precision is slower. Consequently, it is often only used if necessary. – Bob Hanlon Nov 10 '17 at 20:53
5

Another answer copied from Daniel Lichtblau's. I updated it to use WhenEvent instead of EventLocator. The idea is to integrate the derivative of the function and use WhenEvent to detect extrema.

f[y_?NumericQ] = Abs[uu[y]]
vals = Reap[
    soln = y[x] /. First[
      NDSolve[{
        y'[x] == Evaluate[f'[x]],
        y[10] == (f[10]), 
        WhenEvent[y'[x] == 0, Sow[{x, y[x]}]]}, y[x], {x, .5, 30}]]][[2, 1]]

Then plot the function with the points stored in vals:

Plot[f[x], {x, 0, 30}, Epilog -> {PointSize[Medium], Red, Point[vals]}]

enter image description here

It then suffices to select the point of vals with the largest second value (Last[SortBy[vals, Last]]).

anderstood
  • 14,301
  • 2
  • 29
  • 80
3

One can extract the interpolated values from the InterpolatingFunction object, so here is another possibility. I've rewritten your ODE slightly:

sol = NDSolveValue[
    {(u[y] - ω/α)*(ϕ''[y] - α^2*ϕ[y]) - u''[y]*ϕ[y] == 0, ϕ[80] == 1, ϕ'[80] == -I*α},
    ϕ,
    {y, 0, 80}
];
sol //OutputForm

InterpolatingFunction[{{0., 80.}}, <>]

Then, the approximate maximum can be found from:

Max @ Abs @ (sol')["ValuesOnGrid"]

2.63037

This value will be slightly lower than the real maximum because the maximum probably occurs between grid points.

Carl Woll
  • 130,679
  • 6
  • 243
  • 355
2
vv[y_] := ϕ'[y] Conjugate[ϕ'[y]];
min = FindMaximum[{vv[t], 0. <= t <= 80}, {t, 2.6}]
Sqrt[min[[1]]]

{6.91936, {t -> 5.00765}}

2.63047

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
Henrik Schumacher
  • 106,770
  • 7
  • 179
  • 309
  • But in this case I have to give an aproximation for "t" and the function FindMaximum gives then a local maximum. Is there a way to catch the global maximum without give an aproximation for 't'? – Mateus Nov 10 '17 at 20:18