Finding multiple minimum values

Question

If I have this function (just and example)

 Plot3D[-Abs[Cos[ y] Sqrt[x] Sqrt[ y] Cos[ x]], {x, 0, 20}, {y, 0, 20}]

I am interested in finding the locations of the smallest (minimum) 6 values of this function? How can I do that. Apparently, Findminimum and its likes give me one value.

Thanks for help.

The absolute value is troublesome. Is your actual function like this, where the function values are all nonpositive? — J. M.'s missing motivation, Nov 15 '17 at 05:15
Replacing Abs by Function[x,x^2] leads to a smooth function with the same critical points. — Henrik Schumacher, Nov 15 '17 at 06:21
@qahtah Are you aware that you can accept answers? It's the best way of saying "thanks". See this help page for more details. I ask because you've asked six questions on Mathematica SE, but not accepted a single answer. If none of them have been satisfactory, then that's fair enough, but please consider it. — aardvark2012, Nov 15 '17 at 23:55

aardvark2012 · Answer 1 · 2017-11-15T12:51:13.263

Depending on how similar your actual function is to your example, you could try giving FindMinimum (see below) or FindArgMin a range of reasonable starting values and then just pick the ones you need.

f[x_, y_] := -Abs[Cos[y] Sqrt[x] Sqrt[y] Cos[x]]

sol = FindArgMin[{f[x, y], {x, y} ∈ Rectangle[{0, 0}, {20, 20}]}, 
    {{x, #1}, {y, #2}}] & @@@ Tuples[Range[0, 20, π], 2]

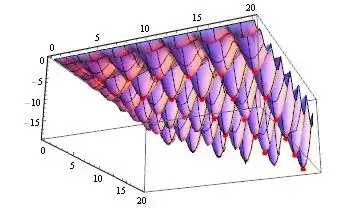
Show[Plot3D[f[x, y], {x, 0, 20}, {y, 0, 20}], 
 Graphics3D[{PointSize[Large], Red, Point[{#1, #2, f[##]} & @@@ sol]}],
 ViewPoint -> {-1.5, -2, 0}]

Then

SortBy[{#1, #2, f[##]} & @@@ sol, Last][[1 ;; 6]]

(* {{18.876, 18.876, -18.8628}, {15.7397, 18.876, -17.222}, {18.876, 15.7397, -17.222}, 
    {15.7397, 15.7397, -15.7239}, {12.606, 18.876, -15.4082}, {18.876, 12.606, -15.4082}} *)

gives you the six minimum values and their locations.

Or alternatively:

sol = FindMinimum[{f[x, y], {x, y} ∈ Rectangle[{0, 0}, {20, 20}]}, 
    {{x, #1}, {y, #2}}] & @@@ Tuples[Range[0, 20, π], 2];
SortBy[sol, First][[1 ;; 6]]

(* {{-18.8628, {x -> 18.876, y -> 18.876}}, {-17.222, {x -> 18.876, y -> 15.7397}}, 
    {-17.222, {x -> 15.7397, y -> 18.876}}, {-15.7239, {x -> 15.7397, y -> 15.7397}}, 
    {-15.4082, {x -> 12.606, y -> 18.876}}, {-15.4082, {x -> 18.876, y -> 12.606}}} *)

and

Show[Plot3D[f[x, y], {x, 0, 20}, {y, 0, 20}], 
 Graphics3D[{PointSize[Large], Red, Point[{x, y, First@#} /. Last@# & /@ sol]}], 
 ViewPoint -> {-1.5, -2, 0}]

gives the same plot. (But I find the Rule format can be a little unwieldy.)

score 4 · Answer 2 · edited Mar 07 '18 at 22:31

Mathematically, it's simple, I think. The function is separable in both axis, so finding the minima along one axis, let say along the $x$-axis, you will have the corresponding ones along the other axis. All the minima in the $xy$-plane will be the combination of both.

Now, along one axis, one function is an monotonic function ($\sqrt{x}$), and the other has the minima, so finding the minima for -Abs[Cos[x]] function (except for $x=0$, as $\cos(0)\sqrt{0}=0$) you will have those you are looking for:

Reduce[Cos[x]] == 1 || Cos[x] == -1 && x >= 0, x]

(* (C[1] ∈ Integers && x == 2 π C[1]) || (C[1] ∈ Integers && ((C[1] >= 1 && 
   x == -π + 2 π C[1]) || (C[1] >= 0 && x == π + 2 π C[1]))) *)

The same for the $y$-axis.

Reduce[Cos[y] == 1 || Cos[y] == -1 && y >= 0, y]

(* (C[1] ∈ Integers && y == 2 π C[1]) || (C[1] ∈ Integers && ((C[1] >= 1 && 
   y == -π + 2 π C[1]) || (C[1] >= 0 && y == π + 2 π C[1]))) *)

All your minima are all the combinations for C[1] and C[2] values:

data = Flatten[
Table[{π + i*π, π + 
  j  π, -Abs[
   Cos[π + i* π] Sqrt[π + i* π] Sqrt[π + 
      j* π] Cos[ π + j* π]]}, {i, 0, 6}, {j, 0, i}], 1] // N;
Show[{Plot3D[-Abs[Cos[y] Sqrt[x] Sqrt[y] Cos[x]], {x, 0, 20}, {y, 0, 
20}, PlotTheme -> "Classic"], pts}]

score 3 · Answer 3 · answered Nov 15 '17 at 16:46

Another idea is to use the MeshFunctions option of ContourPlot[] (as previously shown here) to extract putative positions for the minima, before polishing them with FindMinimum[]:

(* pretend that the function is a black box *)
f[x_?NumericQ, y_?NumericQ] := -Abs[Cos[y] Sqrt[x] Sqrt[y] Cos[x]]

res = Cases[Normal[ContourPlot[Derivative[1, 0][f][x, y] == 0, {x, 0, 20}, {y, 0, 20}, 
                               ContourStyle -> None, Mesh -> {{0}}, 
                               MeshFunctions -> Function[{x, y, z},
                                                         Derivative[0, 1][f][x, y]], 
                               PlotPoints -> 55]], 
            Point[{x0_, y0_}] :> (FindMinimum[{f[x, y], 0 <= x <= 20 && 0 <= y <= 20},
                                              {{x, x0}, {y, y0}}]), ∞];

MinimalBy[DeleteDuplicates[res, First[#1] == First[#2] &], First, 6]
   {{-18.8628, {x -> 18.876, y -> 18.876}}, {-17.222, {x -> 18.876, y -> 15.7397}},
    {-15.7239, {x -> 15.7397, y -> 15.7397}}, {-15.4082, {x -> 18.876, y -> 12.606}},
    {-14.0678, {x -> 12.606, y -> 15.7397}}, {-13.352, {x -> 18.876, y -> 9.47749}}}

(Replace FindMinimum[] with FindMinValue[] or FindArgMin[] if needed.)

Finding multiple minimum values

3 Answers3