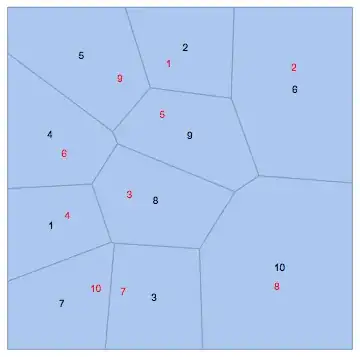
It is not unreasonable to expect that the $k^\text{th}$ cell of a VoronoiMesh belongs to the $k^\text{th}$ point passed to it. However, this is not the case:
SeedRandom[123]
pts = RandomReal[1, {10, 2}];
mesh = VoronoiMesh[pts, MeshCellLabel -> {2 -> "Index"}];
Show[mesh, Graphics[{Red, MapThread[Text, {Range@Length[pts], pts}]}]]
Red: point indices. Black: cell indices.
Is there a direct way to obtain the correspondence between cells and points?
I can do it using some extra computation, but it seems reasonable that this information should be stored somewhere during the construction of the mesh, and therefore shouldn't need to be recomputed at extra cost.
nf = Nearest[pts -> "Index"];
First@*nf /@ RegionCentroid /@ MeshPrimitives[mesh, 2]
(* {4, 1, 7, 6, 9, 2, 10, 3, 5, 8} *)
On my computer, the VoronoiMesh of 3000 points in the plane is computed in 0.1 seconds. But obtaining the cell-point correspondence using the above method takes 4 seconds.
Update:
The key to the solution is given by @kglr in this answer. Use
Flatten @ Nearest[pts -> "Index"] @ PropertyValue[{mesh, 2}, MeshCellCentroid]
The timing is negligible compared to computing the Voronoi tessellation itself. Demonstration:
SeedRandom[123]
pts = RandomReal[1, {10000, 2}];
AbsoluteTiming[mesh = VoronoiMesh[pts];]
(* {0.628788, Null} *)
AbsoluteTiming[
Flatten @ Nearest[pts -> "Index"] @ PropertyValue[{mesh, 2}, MeshCellCentroid];
]
(* {0.003148, Null} *)