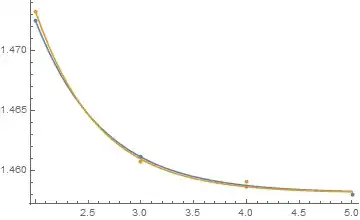
I am aware that similar questions have been asked previously. I am new to Mathematica. I tried all the suggested solutions but unfortunately did not manage to solve my problem. Any help would be highly appreciated.
I have two extremely small datasets:
dat1={{2, 1.4725}, {3, 1.4612}, {4, 1.4587}, {5, 1.4580}}
dat2={{2, 1.4733}, {3, 1.4608}, {4, 1.4591}}
I have two models:
mod1 = a + b Exp[-c x]
mod2 = a + d Exp[-e x]
The parameter a has to be the same for both the models, but needs to be obtained from fitting dat1 and dat2 to mod1 and mod2, respectively. How do I find an optimal fit for all five parameters {a,b,c,d,e} from these two small data sets?