I want to solve a system of Pde (2D) reaction diffusion type using NDSolve
whose boundary conditions are
and the initial conditions are
or
I thought of the following code
(*parameters*)
L = 5;
T = 10;
(*system of nonlinear PDE*)
pde = {D[N1[t, x, y], t] ==
D[N1[t, x, y], x, x] +
D[N1[t, x, y], y,
y] + (1 - N1[t, x, y] - 0.5 N2[t, x, y]) N1[t, x, y],
D[N2[t, x, y], t] ==
D[N2[t, x, y], x, x] +
D[N2[t, x, y], y,
y] + (1 - N2[t, x, y] - 0.5 N1[t, x, y]) N2[t, x, y]};
(*periodic boundary condition*)
bc = {N1[t, -L, y] == N1[t, L, y], N1[t, x, -L] == N1[t, x, L],
N2[t, -L, y] == N2[t, L, y], N2[t, x, -L] == N2[t, x, L]};
(*initial condition*)
ic = {N1[0, x, y] == If[-0.5 <= x <= 1 && -0.5 <= y <= 1, 1, 0],
N2[0, x, y] == If[-0.5 <= x <= 1 && -0.5 <= y <= 1, 0, 1]};
eqns = Flatten@{pde, bc, ic};
{N1, N2} =
NDSolve[eqns, {N1, N2}, {t, 0, T}, {x, -L, L}, {y, -L, L},
Method -> {"MethodOfLines",
"SpatialDiscretization" -> {"TensorProductGrid"}}]
However, the following errors appear.
Also, when constructing the plot (by DensityPlot), I verify that there is a failure in the initial condition, as shows
Can someone help me?
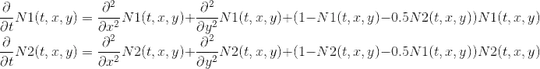





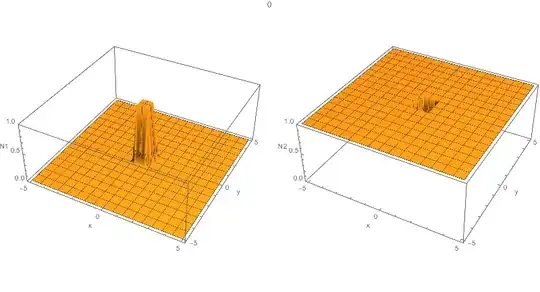
{solN1, solN2} = NDSolveValue[……instead of{N1, N2} = NDSolve[…. 2. TryPlot3Dinstead ofDensityPlot, or setting a largerPlotPointsforDensityPlot.