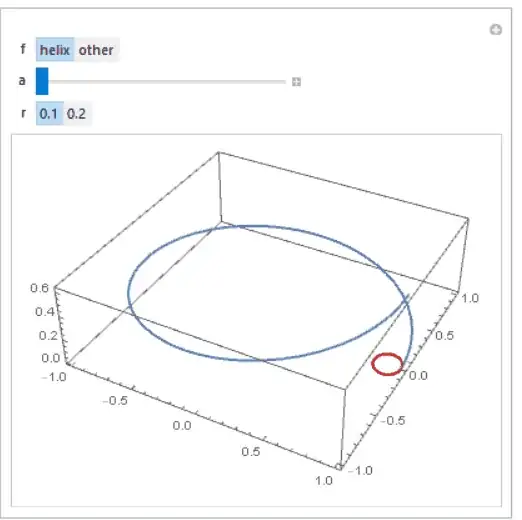
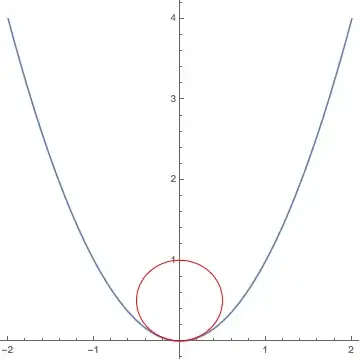
How create an animation of osculation circle to a parametric curve with below circle3D:
circle3D[centre_: {0, 0, 0}, radius_: 1, normal_: {0, 0, 1},
angle_: {0, 2 Pi}] :=
Composition[
Line,
Map[RotationTransform[{{0, 0, 1}, normal}, centre], #] &, Map[Append[#, Last[centre]] &, #] &,
Append[DeleteDuplicates[Most[#]], Last[#]] &,
Level[#, {-2}] &,
MeshPrimitives[#, 1] &,
DiscretizeRegion,
If
][First[Differences[angle]] >= 2 Pi,
Circle[Most[centre], radius],
Circle[Most[centre], radius, angle]
]