Show a gif of polynomial equations' roots

Question

I want to show the solutions of polynomial equations $P_n(x)=y$.

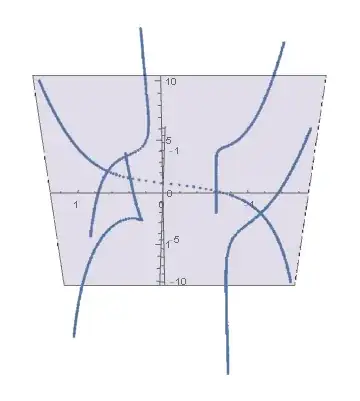
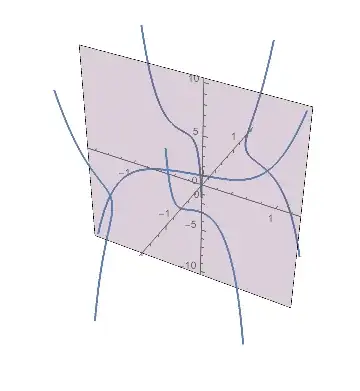
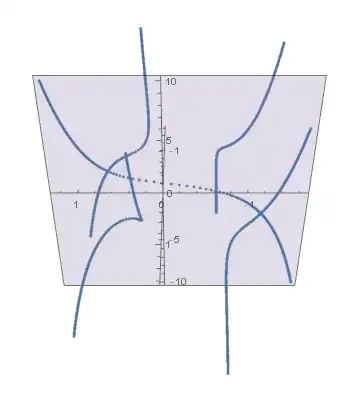
For example, let $P_5(x)=x^5+x^4+x^3+x^2+1=y\ ,\;y\in[-10,10]$,

sol[i_,j_]:=Join[#,{i}]&/@ReIm[x/.NSolve[x^5+x^4+x^3+x+1==i+j I]];
p=Graphics3D[{Opacity[0.25],InfinitePlane[{{0,0,1},{1,0,1},{1,0,0}}]}];
gifs=Table[Show[
    ListPointPlot3D[Flatten[Table[sol[i,0],{i,-10,10,0.1}],1],
    BoxRatios->{1,1,1},AxesOrigin->{0,0,0},Boxed->False,
    ViewPoint->{2Sin[t],2Cos[t],1.5}],p],
    {t,0,2Pi,0.1}];
Export["poly5.gif",gifs, "AnimationRepetitions"->Infinity]

Oh...terrible, the image is constantly shaking, at least the origin point should be fixed.

Secound, I want to get the curves instead of points, $n$ curves when $P_n(x)$. I can only get points if I use NSolve.

Then I can dye according to their distance from the plane, I mean real plane XoY, the distance equal to imaginary part.

And if the curve on that plane, use special colour like red. If the curve just cross the plane, also highlight that point red.

What happens if you add the option SphericalRegion -> True? — Michael E2, Dec 11 '17 at 12:06

Chris K · Accepted Answer · 2017-12-12T02:08:12.803

Here's another piece of the puzzle, specifically how to get continuous lines instead of points by using Solve and ParametricPlot3D.

p = Graphics3D[{Opacity[0.25], InfinitePlane[{{0, 0, 1}, {1, 0, 1}, {1, 0, 0}}]}];
sol = Solve[x^5 + x^4 + x^3 + x + 1 == y, x]
(* five Root solutions *)
Show[p,
  ParametricPlot3D[Append[ReIm[x], y] /. sol, {y, -10, 10}], 
  BoxRatios -> {1, 1, 1}, AxesOrigin -> {0, 0, 0}, Boxed -> False, Axes -> True]

Mathematica graphics

Animated:

Animated

EDIT:

GalAster points out that this approach has a problem with another polynomial x^4 + x^3 - 2 x - 1.

sol = Solve[x^4 + x^3 - 2 x - 1 == y, x, Quartics -> False]
(* four Root solutions *)
Show[p,
  ParametricPlot3D[Append[ReIm[x], y] /. sol, {y, -10, 10}], 
  BoxRatios -> {1, 1, 1}, AxesOrigin -> {0, 0, 0}, Boxed -> False, Axes -> True,
  , AxesLabel -> {"Re", "Im", "y"}]

Mathematica graphics

Indeed, this has some spurious connectors when the bifurcation occurs and the roots change order. Evidently a well-placed Evaluate fixes this problem.

Show[p,
  ParametricPlot3D[Evaluate[Append[ReIm[x], y] /. sol], {y, -10, 10}, MaxRecursion -> 12],
  BoxRatios -> {1, 1, 1}, AxesOrigin -> {0, 0, 0}, Boxed -> False, Axes -> True,
  AxesLabel -> {"Re", "Im", "y"}]

Mathematica graphics

Wow, Root can be used like this! A small commit, Solve[P, x, Quartics -> False, Cubics -> True] or something terrible would happen on some cases. — Aster, Dec 12 '17 at 01:21
Well, not solved, still have problem, try x^4 + x^3 - 2 x - 1 — Aster, Dec 12 '17 at 01:26

score 4 · Answer 2 · answered Dec 11 '17 at 18:59

4

This answers the shaking part. As @Michael E2 said, if you add SphericalRegion -> True the shaking goes away

This animation with SphericalRegion -> True

This is without

answered Dec 11 '17 at 18:59

Nasser

143,286
11
154
359

Show a gif of polynomial equations' roots

2 Answers2