0

I am trying to evaluate a numerical integral and running into slow convergence issues. My problem is as follows: I have a 6x6 Hermitian matrix, H[x,y], whose elements are functions of two parameters x and y. I find the eigenvalues of this matrix, which are real

eigs[x_, y_] := Eigenvalues[H[x, y]]

and expressed using the Root function as roots of 6th degree polynomials.

I also have a function

df[m_, e_, t_] := 1/(2 t + 2 t Cosh[(e - m)/t])

which some may recognize as the derivative of the Fermi Dirac function -- for small values of t, it is very sharply peaked at e == m. My integrand is df[m,eigs[x, y], t] for some value of m and t, say for example:

NIntegrate[df[0, eigs[x, y], .1] // Total, {x, xmin, xmax},{y, ymin, ymax}]

I can plot the integrand and it is sharply peaked along contours within the limits of integration (where one or another of the eigenvalues equals m), but I am having some trouble getting the integral to converge efficiently--I get slow convergence errors, or nonsense answers if I try to decrease accuracy and precision goals.

Any advice? Looking at the points from the evaluation monitor, the LocalAdaptive method seems to find the correct areas to integrate but still takes a long time (around 30 seconds on my laptop with MaxRecursion->3) and fails to converge.

Edit

Here is an example of H[x, y]:

H[x_, y_] := 
  {{24, 1550 Sqrt[3] (x + I y), 100, 0, 0, 0}, 
   {1550 Sqrt[3] (x - I y), 31, 0, 0, 0, 100}, 
   {100, 0, -4, 315 Sqrt[3/2] (x - I y), -41 Sqrt[3/2] (x + I y), 1550 Sqrt[3] (x + I y)}, 
   {0, 0, 315 Sqrt[3/2] (x + I y), -20, 1550 Sqrt[3] (x - I y), -41 Sqrt[3/2] (x - I y)}, 
   {0, 0, -41 Sqrt[3/2] (x - I y), 1550 Sqrt[3] (x + I y), 26, 390 Sqrt[2]}, 
   {0, 100, 1550 Sqrt[3] (x - I y), -41 Sqrt[3/2] (x + I y), 390 Sqrt[2], 81}}

I would be interested in the integral of the eigenvalues for values of m between -100 and 100, which corresponds to limits of the integral of around +/-.2 for both x and y

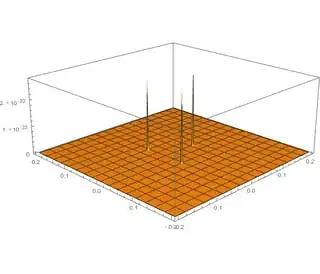
The integrand (This takes a long time with PlotPoints -> 1000)

Plot3D[Total[df[0, eigs[x, y], 1/10]], {x, -.2, .2}, {y, -.2, .2}, 
  PlotPoints -> 1000]

enter image description here

Community
  • 1
Andrea
  • 1
  • 1
  • 2
    Can you add the code for H[x,y]? Or at least a minimal working equivalent. It will make it easier for people to figure out what's going on. – aardvark2012 Dec 13 '17 at 06:34
  • aardvark2012 and nasser: I added some code for H. Apologies. – Andrea Dec 13 '17 at 20:39
  • I added ranges--b1550 was a typo transcribing the code from mathematica--it should just read 1550 (corrected now). – Andrea Dec 13 '17 at 21:03
  • Hi George and thanks for your responses. Actually, I want the sum of the function df over all the eigenvalues--so ordering not an issue in the final result. It doesn't seem to matter that much for convergence whether I sum them or try to integrate just one of them. – Andrea Dec 13 '17 at 21:19
  • In the range of m I'm interested in, usually 4-5 of the eigenvalues give basically zero, but as you notice its hard to tell which ones that will be given ordering. – Andrea Dec 13 '17 at 21:23
  • Related: https://mathematica.stackexchange.com/questions/107416/using-nintegrate-to-integrate-functions-with-sharp-peaks-lorentzian-like – Michael E2 Dec 13 '17 at 21:32
  • fyi it is much faster if you make H numeric : H[x_?NumericQ, y_?NumericQ] := N[..., 20] (and set precision there ). Be sure to make your t exact if you work in extended precision. ) – george2079 Dec 13 '17 at 22:25
  • @george2079, making H numeric and reducing the accuracy and precision goals of NIntegrate seems to help a lot. I don't understand your comment about making t exact though--where can I read about how this works for NIntegrate (in other words, where I should be setting things to be numeric and where exact)? – Andrea Dec 15 '17 at 03:43

0 Answers0