5

This question is motivated by considering different alternative answers to this question.

More specifically, this question intends to investigate what appears to be an unexpected outcome (at least, unexpected by me).

This unexpected outcome has to do with the relative effectiveness of using two built-in symbols/functions to answer the linked question, namely using a combination of Map and Rest against using just Drop.

The intuition, from working knowledge of the language, was that using Map would be in general less efficient than using Drop. This intuition was verified by applying the relevant approaches to the question's input.

I will replicate the input from that question and the two proposed approaches for the purpose of providing this question with an appropriate context

x = {{{1, 2}, {4, 5, 6}, {7, 8, 9}}, {{10, 11}, {13, 14, 15}, {16, 17, 18}}};

{tMap,resMap} = Map[Rest, x] // RepeatedTiming;

{tDrop, resDrop} = Drop[x, None, 1] // RepeatedTiming;

tMap / tDrop

returns 3., as expected.

Going a step further, to confirm the intuition, I sought to replicate the results. The test setup I used, is provided in the end of this question.

The gist of it was to generate a number of use-case similar to the input and use several proposed approaches in order to gauge which performed best.

An assumption in the test set up was that the source of variance in the input is mostly due to the dimension in level 1. Longer lists in level 1 would (supposedly) imply more applications of Rest and hence more time. Similar considerations were related to the application of Drop (I assumed, Drop works in an analogous fashion).

To make a long story short, it turns out that my intuition was wrong.

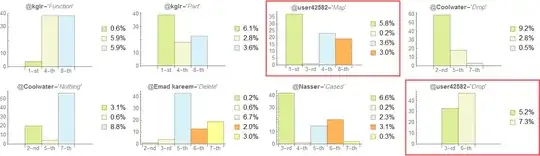
enter image description here

The collection of graphs above summarizes the results of a single run of testing 8 proposed solutions on 640 discrete use cases. As anyone can see in the highlighted bar-charts, Drop is the third best performing solution in 5.2% of the test cases while Map is the first best performing solution in 5.8% of the use cases.

These ranking change between different runs of the tests but they seem to be consistent in that Map out-performs Drop (another feature seems to be that Part appears to be a better choice, in general).

In light of these findings and conditional upon the nature of the task at hand (dropping the first entry in a list of lists) is it safe to assume that using Map is a better choice than using Drop most of the time (and using Part is probably the best choice in general) ?

code can be found here

edit: updated graphs/changed implementation of a function as indicated in the comments;

enter image description here

edit #2: updated graphs after correction suggested by @Coolwater (thank you)

enter image description here

note: this correction answers the question in the negative: Map is not counterintuitively faster than Drop; in fact, changing the code as suggested verifies initial intuition; additionally, it seems that Part is indeed a good choice (along with using Drop as originally suggested by @Coolwater).

user42582
  • 4,195
  • 1
  • 10
  • 31
  • I haven't looked carefully at your code, but is it possible that sometimes the lists that you are generating are packed and sometimes they're not? That might make a difference. – march Dec 13 '17 at 19:23
  • no, at least, not explicitly or intentionally; the testing is done on random integer lists with dimensions from Outer[List,{2, 10, 100, 500, 1000},{3, 5, 7, 9},{3, 5, 7, 9},1] – user42582 Dec 13 '17 at 20:24
  • I don't think kglr's Function variant is fairly tested: you're wrapping the assignment of the function to the symbol inside a Module and doing repeated timing on the whole thing instead of just \[HappySmiley]@x // RepeatedTiming. It's a bit tedious to make out the details of your test code to comment on its validity, but are you only working on packed arrays? What if there's a ragged array? Does it matter if sublists are packed? Lot's of hard-to-compare edge cases. The relative amount of times one approach or another came first doesn't tell me much. What about their actual run times? – LLlAMnYP Dec 14 '17 at 08:18
  • changed the implementation as suggested; 2. with all due respect I'd consider my code fairly straightforward; I'd happily accept pointers 3. I'm not using packed arrays explicitly 4. ragged arrays would make things worse for all approaches; they were not in the context of the question that motivated the testing; 5. how are integer lists of varying length "edge-cases" 6. absolute times are easily obtained from my code; why are ranks not relevant for comparisons of relative performance (what I'm trying to do)?
    • – user42582 Dec 14 '17 at 08:59