How to add a point and drag it into position in a 3D plot?

Question

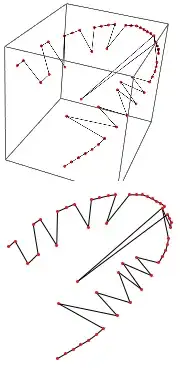
I have some plotted points and I would like to add new points and be able to drag a pre-existing or added point using my mouse. After I am satisfied with the new plot, I would like to extract the coordinates of the points. Adding new points is not as important as being able to drag points already present.

Any ideas?.

pt = List @@@ ColorData["ThermometerColors"] /@ Subdivide[50];
Show[ListPointPlot3D[pt, BoxRatios -> {1, 1, 1}, ImageSize -> Medium, 
   PlotStyle -> {Red, PointSize[0.015]}, 
   AxesLabel -> {"Red", "Green", "Blue"}] /. 
  Point[x_] :> {Tooltip[Point[#], #] & /@ x}, Graphics3D@Line@pt]

Points are taken from

I have edited points manually and I have got this plot which is more or less what I want, but I would prefer a smoother curve.

My ultimate goal is to get more blue and red at the end points and keep middle as "ThermometerColors"

Do you always expect your points to define a plane? If so, this problem is tractable. If not, the 2D motion of your mouse cannot easily be correlated with a 3D motion. — b3m2a1, Dec 17 '17 at 01:23
related/relevant: How can locators be added to the points on a 3D grid? — kglr, Dec 17 '17 at 01:34
Your example data actually doesn't define one, interestingly. I'll provide a partial answer to the no plane case and see if it works well enough for you. — b3m2a1, Dec 17 '17 at 01:43

score 8 · Accepted Answer · answered Dec 17 '17 at 04:48

This is not a complete answer (nor a robust one, likely), but here's one option (basic method stolen from @Heike's answer here).

Some notes on adding new points:

For adding points, I used a right-click event so as not to interfere with the built-in pan/zoom/rotate for Graphics3D (I'm sure there's an obvious "nicer" way to do this, but this works for now).
As @b3m2a1 noted, it's not really an easy thing to pick out a particular point in the 3D space with the mouse position. MousePosition["Graphics3DBoxIntercepts"] can give us the endpoints of the line of points a single mouse click could potentially map to (as shown in this answer), but one would still have to give the program the desired "depth" somehow. However, since we are able to move the points after the fact, we can simply choose the "front" coordinate of MousePosition["Graphics3DBoxIntercepts"] and adjust as necessary. (Again, probably not optimal, but the best I can think of at the moment.)
The points can only be added to the ends of the curve at the moment (the Setter at the bottom determines which end).

initpts = List @@@ ColorData["ThermometerColors"] /@ Subdivide[50];

DynamicModule[
 {pts = initpts,
  current,
  icurrent,
  prepending = False,
  newpt
  },

 Column[{
   EventHandler[
    Graphics3D[{
      EventHandler[
       Dynamic@{
         {PointSize[0.015],
          Red,
          Tooltip[Point[#], #] & /@ pts},
         Line[pts]
         },
       {
        "MouseDown" :> (

          current = 
           Nearest[pts, MousePosition["Graphics3DBoxIntercepts"]][[1, 
             1]];
          icurrent = First@Flatten@Position[pts, current]),
        "MouseDragged" :> (

          pts[[icurrent]] = (#[[2]] + 
               Projection[
                current - #[[2]], #[[1]] - #[[2]]]) &@(MousePosition[
              "Graphics3DBoxIntercepts"])
          )
        }
       ]
      },
     ImageSize -> {400, Automatic},
     Axes -> True,
     AxesLabel -> {"Red", "Green", "Blue"}
     ],
    {{"MouseClicked", 2} :> (
       newpt = First@MousePosition["Graphics3DBoxIntercepts"];
       If[
        prepending,
        PrependTo[pts, newpt],
        AppendTo[pts, newpt]
        ]
       )}
    ],
   Row@{Setter[Dynamic[prepending], True, "Prepend new points"], 
     Setter[Dynamic[prepending], False, "Append new points"]},
   OpenerView[{"Current Points", Dynamic@pts}]
   }]
 ]

Thank you all, problem is harder than I thought but your codes helped me a lot. — OkkesDulgerci, Dec 17 '17 at 16:47

score 6 · Answer 2 · answered Dec 17 '17 at 02:07

Here's a way to make a locator pane that allows you to move your points in the plane of the current ViewMatrix:

pt = List @@@ ColorData["ThermometerColors"] /@ Subdivide[50];
transf =
  {{1.1`, 0.4`, 0.`, -0.8`}, {-0.2`, 0.5`, 1.`, -0.7`}, {-0.4`, 
    1.`, -0.5`, 3.4`}, {0.`, 0.`, 0.`, 1.`}};
proj =
  {{2.2`, 0.`, 0.5`, 0.`}, {0.`, 2.2`, 0.5`, 0.`}, {0.`, 0.`, 
    4.3`, -13.8`}, {0.`, 0.`, 1.`, 0.`}};

Column@{
  Graphics3D[
   {
    {Red, Point[Dynamic[pt]]},
    Line@Dynamic[pt]
    },
   ViewMatrix -> Dynamic[{transf, proj}],
   ImageSize -> Large
   ],
  Dynamic[
   With[{tf = transf[[;; 3, ;; 3]], 
     inv = Inverse[transf[[;; 3, ;; 3]]]},
    Graphics[
     {
      Line[Dynamic[Transpose[tf.Transpose[pt]][[All, ;; 2]]]],
      {Red, 
       Point[Dynamic[Transpose[tf.Transpose[pt]][[All, ;; 2]]]]},
      Table[
       With[{i = i},
        Locator[
         Dynamic[
          Dot[tf, pt[[i]]][[;; 2]],
          Function[pt[[i]] = inv.Append[#, 0]]
          ],
         None
         ]
        ],
       {i, Length@pt}
       ]
      }
     ]
    ]
   ]
  }

It really emphasizes how tricky the concept of a 2D motion in a 3D space can be.

These 2D motions appear one way, but rotation of the 3D object shows that the true motion can be very different from the apparent one.

If your points define a plane, simply find the transformation that rotates this plane to the xy plane and have your locators live there. Then, obviously, when setting values apply the inverse of this transformation.

How to add a point and drag it into position in a 3D plot?

2 Answers2

Linked