The trace on my plot goes beyond the domain of the function plotted

Question

Here's the domain of the function:

When I'm trying to plot it Mathematica just shows a graph of $x+1$.

Here's what happens if we put $x$ in formula from outside of a function's domain:

I'm not sure whether it's a bug or Mathematica simplifies the equation to $x+1$ but I'm searching for a way to plot it correctly. Any help would be appreciated!

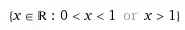
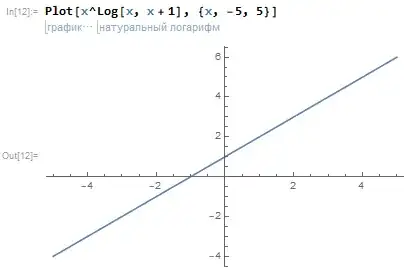
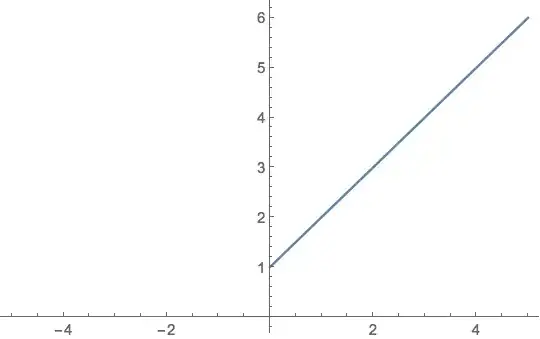
If I just input x^Log[x, x + 1] Mathematica returns 1 + x. So I think it's a simplification thing. You could use Plot[x^Log[x, x + 1], {x, -5, 5}, RegionFunction -> Function[{x}, 0 < x < 1 || x > 1]] to get it plotting over the domain you want. — aardvark2012, Dec 21 '17 at 20:34
Even without simplification mathematica gladly works in the complex domain, Log[-5, -4] // N -> 0.971177 + 0.0562626 I then (-5)^(0.971177 + 0.0562626 I) -> -4+eps I — george2079, Dec 21 '17 at 20:51
You can tell MA that Logshould be real: Plot[x^Re[Log[x, x + 1]], {x, -5, 5}], although it is not quite the same. — yarchik, Dec 21 '17 at 20:53
I claim that MA correctly plots this function, because the FunctionDomain is the whole real axis. Maybe you are concerned that intermediate steps are only possible in your domain. However, this is not right mathematical logic: have a look at $sin(x)=(e^{ix}+e^{-ix})/2i$---the result is real although each exponent is complex for each real $x$. — yarchik, Dec 21 '17 at 21:13
Evaluation of x^Log[x, x + 1] expression to 1 + x is "generically correct" for Power and Log as functions of complex arguments, which is how they are defined in Mathematica. You could use my RestrictDomain function: RestrictDomain[x^Log[x, x + 1], x, Reals] to get expression with domain restriction, assuming all functions are restricted to Reals. — jkuczm, Dec 22 '17 at 20:46

score 4 · Answer 1 · answered Dec 21 '17 at 21:24

4

Clear[f]

f[x_] := x^Log[x, x + 1] /; 0 < x < 1 || x > 1;

f /@ {-5, 0, 1, 5}

(* {f[-5], f[0], f[1], 6} *)

Plot[f[x], {x, -5, 5}, AxesOrigin -> {0, 0}]

answered Dec 21 '17 at 21:24

Bob Hanlon

157,611
7
77
198

score 3 · Accepted Answer · edited Dec 22 '17 at 19:45

Assuming e.g. a real functions realm one could expect what you expect. But there is no straightforward way to do so and in expressions + complexes world it is correct.

The problem is that there is no FunctionFormula expression with special rules in Mathematica so your example will be simplified automatically.

Fortunately FunctionDomain handles uneavaluated formula well:

FunctionDomain[Unevaluated[x^Log[x, x + 1]], x]

0 < x < 1 || x > 1

Plot[
  x^Log[x, x + 1]
, {x, -10, 10}
, RegionFunction -> Function[
    x
  , Evaluate@FunctionDomain[Unevaluated[x^Log[x, x + 1]], x]
  ]
]

The trace on my plot goes beyond the domain of the function plotted

2 Answers2