Table of precedence values for all System` symbols

Question

Has anyone created a table listing the precedences for all symbols? Also, it would be nice if there were a function that for a given precedence value or interval, returned all the symbols with that precedence. This list of precedences would be useful when trying to decide on an operator form without built-in meaning.

Also related, perhaps duplicate: (135805) – Mr.Wizard Mar 02 '18 at 15:38 — Mr.Wizard, Mar 02 '18 at 15:38

score 11 · Answer 1 · answered Dec 22 '17 at 21:01

You can use Precedence to get the precedence for a symbol. The following code produces an association with precedences as keys, and symbol names corresponding to that precedence as values:

precedenceAssociation = KeySort @ GroupBy[
    Names["System`*"],
    ToExpression[#,StandardForm, Function[Null, Precedence[Unevaluated[#]],HoldAll]]&
];
Normal @ KeyDrop[670.] @ precedenceAssociation

{0. -> {"OverBar", "OverDot", "OverHat", "OverTilde", "OverVector", "SubMinus", "SubPlus", "SubStar", "SuperDagger", "SuperMinus", "SuperPlus", "SuperStar", "UnderBar"}, 10. -> {"CompoundExpression"}, 20. -> {"ColonForm"}, 30. -> {"Put", "PutAppend"}, 40. -> {"Set", "SetDelayed", "UpSet", "UpSetDelayed"}, 50. -> {"Because", "Therefore"}, 60. -> {"VerticalSeparator"}, 70. -> {"Postfix"}, 80. -> {"Colon"}, 90. -> {"Function"}, 100. -> {"AddTo", "DivideBy", "SubtractFrom", "TimesBy"}, 110. -> {"ReplaceAll", "ReplaceRepeated"}, 120. -> {"Rule", "RuleDelayed"}, 125. -> {"TwoWayRule"}, 130. -> {"Condition"}, 135. -> {"StringExpression"}, 140. -> {"Optional"}, 150. -> {"Pattern"}, 160. -> {"Alternatives"}, 170. -> {"Repeated", "RepeatedNull"}, 180. -> {"SuchThat"}, 190. -> {"DoubleLeftTee", "DoubleRightTee", "DownTee", "LeftTee", "Perpendicular", "RightTee", "UpTee"}, 195. -> {"Conditioned"}, 200. -> {"Implies"}, 205. -> {"Equivalent"}, 215. -> {"And", "Nand", "Nor", "Or", "Xnor", "Xor"}, 230. -> {"Not"}, 240. -> {"Exists", "ForAll", "NotExists", "RoundImplies"}, 250. -> {"Distributed", "Element", "NotElement", "NotReverseElement", "NotSquareSubset", "NotSquareSubsetEqual", "NotSquareSuperset", "NotSquareSupersetEqual", "NotSubset", "NotSubsetEqual", "NotSuperset", "NotSupersetEqual", "ReverseElement", "SquareSubset", "SquareSubsetEqual", "SquareSuperset", "SquareSupersetEqual", "Subset", "SubsetEqual", "Superset", "SupersetEqual"}, 270. -> {"DoubleLeftArrow", "DoubleLeftRightArrow", "DoubleRightArrow", "DownLeftRightVector", "DownLeftTeeVector", "DownLeftVector", "DownLeftVectorBar", "DownRightTeeVector", "DownRightVector", "DownRightVectorBar", "LeftArrow", "LeftArrowBar", "LeftArrowRightArrow", "LeftRightArrow", "LeftRightVector", "LeftTeeArrow", "LeftTeeVector", "LeftVector", "LeftVectorBar", "LowerLeftArrow", "LowerRightArrow", "RightArrow", "RightArrowBar", "RightArrowLeftArrow", "RightTeeArrow", "RightTeeVector", "RightVector", "RightVectorBar", "ShortLeftArrow", "ShortRightArrow", "UpperLeftArrow", "UpperRightArrow"}, 280. -> {"DoubleVerticalBar", "NotDoubleVerticalBar", "NotVerticalBar", "VerticalBar"}, 290. -> {"Congruent", "CupCap", "DotEqual", "Equal", "EqualTilde", "Equilibrium", "Greater", "GreaterEqual", "GreaterEqualLess", "GreaterFullEqual", "GreaterGreater", "GreaterLess", "GreaterTilde", "HumpDownHump", "HumpEqual", "LeftTriangle", "LeftTriangleBar", "LeftTriangleEqual", "Less", "LessEqual", "LessEqualGreater", "LessFullEqual", "LessGreater", "LessLess", "LessTilde", "NestedGreaterGreater", "NestedLessLess", "NotCongruent", "NotCupCap", "NotEqualTilde", "NotGreater", "NotGreaterEqual", "NotGreaterFullEqual", "NotGreaterGreater", "NotGreaterLess", "NotGreaterSlantEqual", "NotGreaterTilde", "NotHumpDownHump", "NotHumpEqual", "NotLeftTriangle", "NotLeftTriangleBar", "NotLeftTriangleEqual", "NotLess", "NotLessEqual", "NotLessFullEqual", "NotLessGreater", "NotLessLess", "NotLessSlantEqual", "NotLessTilde", "NotNestedGreaterGreater", "NotNestedLessLess", "NotPrecedes", "NotPrecedesEqual", "NotPrecedesSlantEqual", "NotPrecedesTilde", "NotRightTriangle", "NotRightTriangleBar", "NotRightTriangleEqual", "NotSucceeds", "NotSucceedsEqual", "NotSucceedsSlantEqual", "NotSucceedsTilde", "NotTilde", "NotTildeEqual", "NotTildeFullEqual", "NotTildeTilde", "Precedes", "PrecedesEqual", "PrecedesSlantEqual", "PrecedesTilde", "Proportion", "Proportional", "ReverseEquilibrium", "RightTriangle", "RightTriangleBar", "RightTriangleEqual", "SameQ", "Succeeds", "SucceedsEqual", "SucceedsSlantEqual", "SucceedsTilde", "Tilde", "TildeEqual", "TildeFullEqual", "TildeTilde", "Unequal", "UnsameQ"}, 295. -> {"DirectedEdge", "UndirectedEdge"}, 300. -> {"IntervalIntersection", "IntervalUnion", "SquareUnion", "Union", "UnionPlus"}, 305. -> {"Intersection", "Span", "SquareIntersection"}, 310. -> {"Complex", "MinusPlus", "Plus", "PlusMinus", "Subtract"}, 320. -> {"DiscreteLimit", "DiscreteMaxLimit", "DiscreteMinLimit", "Limit", "MaxLimit", "MinLimit", "Sum"}, 325. -> {"ExpectationE", "Integrate", "ProbabilityPr"}, 330. -> {"CircleMinus", "CirclePlus"}, 340. -> {"Cup"}, 350. -> {"Cap"}, 360. -> {"Coproduct"}, 370. -> {"VerticalTilde"}, 380. -> {"ContinuedFractionK", "Product"}, 390. -> {"Star"}, 395. -> {"Mod"}, 400. -> {"Times"}, 410. -> {"CenterDot"}, 420. -> {"CircleTimes"}, 430. -> {"Vee"}, 440. -> {"Wedge"}, 450. -> {"Diamond"}, 460. -> {"Backslash"}, 470. -> {"Divide"}, 480. -> {"Minus", "Piecewise"}, 490. -> {"Dot"}, 495. -> {"TensorProduct"}, 500. -> {"Cross", "TensorWedge"}, 510. -> {"NonCommutativeMultiply"}, 520. -> {"CircleDot", "PermutationProduct"}, 530. -> {"SmallCircle"}, 540. -> {"Square"}, 550. -> {"CapitalDifferentialD", "D", "Del", "DifferenceDelta", "DifferentialD", "DiscreteRatio", "DiscreteShift", "Divergence", "Dt", "Gradient"}, 580. -> {"DoubleDownArrow", "DoubleLongLeftArrow", "DoubleLongLeftRightArrow", "DoubleLongRightArrow", "DoubleUpArrow", "DoubleUpDownArrow", "DownArrow", "DownArrowBar", "DownArrowUpArrow", "DownTeeArrow", "LeftDownTeeVector", "LeftDownVector", "LeftDownVectorBar", "LeftUpDownVector", "LeftUpTeeVector", "LeftUpVector", "LeftUpVectorBar", "LongLeftArrow", "LongLeftRightArrow", "LongRightArrow", "ReverseUpEquilibrium", "RightDownTeeVector", "RightDownVector", "RightDownVectorBar", "RightUpDownVector", "RightUpTeeVector", "RightUpVector", "RightUpVectorBar", "ShortDownArrow", "ShortUpArrow", "UpArrow", "UpArrowBar", "UpArrowDownArrow", "UpDownArrow", "UpEquilibrium", "UpTeeArrow"}, 590. -> {"Power", "SuperscriptBox"}, 600. -> {"StringJoin"}, 610. -> {"Factorial", "Factorial2"}, 620. -> {"Apply", "Map", "MapAll"}, 624. -> {"RightComposition"}, 625. -> {"Composition"}, 630. -> {"Infix"}, 640. -> {"InvisibleApplication", "Prefix"}, 660. -> {"Decrement", "Increment", "PreDecrement", "PreIncrement"}, 680. -> {"PatternTest"}, 690. -> {"SubsuperscriptBox"}, 695. -> {"SubscriptBox"}, 700. -> {"UnderoverscriptBox"}, 710. -> {"OverscriptBox", "UnderscriptBox"}, 720. -> {"Get"}, 730. -> {"Blank", "BlankNullSequence", "BlankSequence"}, 740. -> {"Slot", "SlotSequence"}, 750. -> {"MessageName"}}

I removed the 670. precedence from the output above, as symbols without an output form all live in that precedence, and are not that interesting (and they take up a lot of space). One can use this association to answer your second question. For instance:

KeySelect[EqualTo[730.]] @ precedenceAssociation
KeySelect[Between[{140, 150}]] @ precedenceAssociation

<|730. -> {"Blank", "BlankNullSequence", "BlankSequence"}|>

<|140. -> {"Optional"}, 150. -> {"Pattern"}|>

I think this is not a complete story. Look at SystemDumpunicodeCharactersTR file, where You will find some character precedences, which are important for constructing Mma expressions. The numbers in the 5-th column are true precedences for these symbols, whereas the numbers returned by Precedence[] command do not play role here. My impression that the story behind how Mma handles precedences is much more complicated. — Acus, Dec 27 '17 at 08:00
@user18792 I agree; I have found the TR file more reliable and complete, and used it for (135805). — Mr.Wizard, Mar 02 '18 at 15:39
I agree that the table produced by Precedence is incomplete, but more importantly in my view, it is also incorrect. It gives the same precedence to many operators that actually have different precedence, and it assigns the wrong precedence to several operators. The unicodeCharactersTR file is also incomplete as it appears to only include operators that are single Unicode characters outside of the ASCII character set. Also, for reasons I don't understand, it seems to be wrong in a small number of cases. — Robert Jacobson, Aug 14 '18 at 20:03
@RobertJacobson If you have examples, it would probably make a good question. — Carl Woll, Aug 14 '18 at 22:45
@CarlWoll It seems to me that making an answer on (135805 is the best thing. — Robert Jacobson, Aug 14 '18 at 23:00
@RobertJacobson I was referring to the wrong precedences, not the missing ones. — Carl Woll, Aug 14 '18 at 23:14
@CarlWoll I have found many errors in the documentation and in Precedence[] while studying Wolfram Language from a programming languages perspective recently. The answer I just posted on (135805) will give you a feel for why I don't think it's worth it to document the errors in an undocumented function that doesn't even give an answer 10% of the time. I suspect Precedence[] is a holdover from some ancient version that just never got removed. People should stop using it. Use WolframLanguageData instead. — Robert Jacobson, Aug 15 '18 at 02:22

Ronald Monson · Answer 2 · 2020-02-20T10:45:16.827

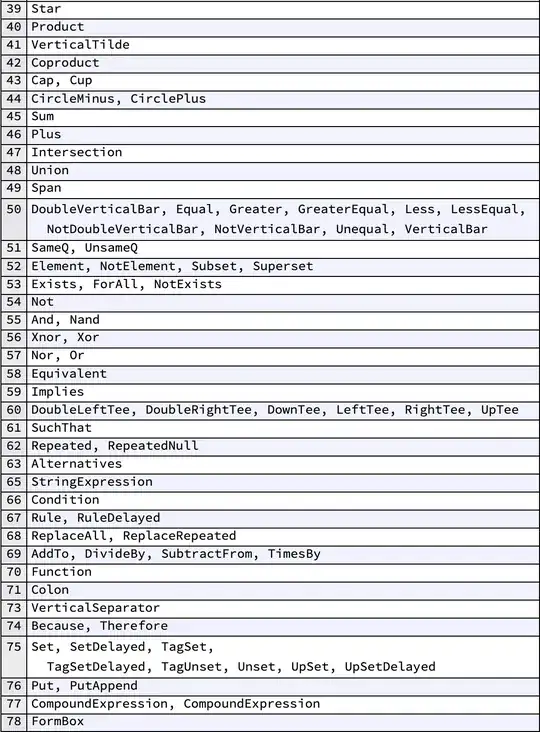
Following up Robert Jacobson's comment to Carl Woll's answer while using Andrew Steinacher's NiceGrid from the FunctionRepository, the following yields a less comprehensive but possibly superseding ranking table:

TightToLooseList = StringRiffle[#, ", "] &/@
GroupBy[WolframLanguageData[All, "PrecedenceRanks"] // 
DeleteMissing, Query[1, -1] -> Query[1, 1], Query[All, Last /* 1 /* 1]] // KeySort;

NiceGrid[TightToLooseList, "MaxNumber" -> 100, Alignment -> Left, Background -> {White, {{White, LightBlue}}}]

Tighter to Looser Bindings:

(WolframLanguageData rankings)

Looser to Tighter Bindings

(WolframLanguageData rankings)

or if you want to juxtapose up in another browser actual Precedence values from Carl Woll's answer

NiceGrid[StringRiffle[#, ", "] & /@ precedenceAssociation, 
 "MaxNumber" -> 100, Alignment -> Left, 
 Background -> {White, {{White, Lighter[Blue, .95]}}}]