Solid of revolution generated with two curves

Question

I'm trying to get the solid of revolution that is generated with two implied curves.The problem say,find the volume of the solid obtained by rotating the region bounded by the curves $x=3y^2-2$ and $x=y^2$ about the line $x=1$. I found a very similar question here, note that I did not know use the RegionPlot3D command, besides I am not sure if it is the correct command for this case. I hope someone can help me get the 3D graphic that is what interests me. Thanks in advance

Area in red is what is rotated around the line $x = 1$

Answer 1

Here is a brute-force way.

1. Find the line segments from the plot

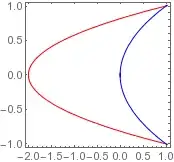
plot = ContourPlot[{(x) == (3 z^2 - 2), (x) == z^2}, {x, -3.5, 3.5}, {z, -1.5, 1.5},
                    MaxRecursion -> 2, RegionFunction -> Function[{x, y}, x <= 1]]
pts = Cases[plot, GraphicsComplex[ps__, __] :> ps, Infinity][[1]];
line = Cases[plot, Line[x_] :> x, Infinity];
lines = pts[[#]] & /@ line;
Graphics[{Red, Line[lines[[1]]], Blue, Line[lines[[2]]]}, Frame -> True, AspectRatio -> 1]

2. Convert it to 3D points and rotate around any desired point or line

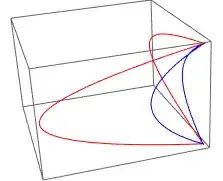
out = {#[[1]], 0.0, #[[2]]} & /@ lines[[1]];
in = {#[[1]], 0.0, #[[2]]} & /@ lines[[2]];
angle = Pi/2;
axis = {0, 0, 1};
point = {1, 0, 0};
out1 = Map[RotationTransform[angle, axis, point], out];
in1 = Map[RotationTransform[angle, axis, point], in];
Graphics3D[{Red, Line[out], Line[out1], Blue, Line[in], Line[in1]}]

3. Rotate over $2\pi$ solid angle to get full surface

out2 = Flatten[Table[Map[RotationTransform[angle,axis,point],out],{angle,0, 2 Pi,0.5}],1];
in2 = Flatten[Table[Map[RotationTransform[angle,axis,point],in],{angle,0, 2 Pi,0.5}], 1];

4. Use ConvexHullMesh

reg1 = ConvexHullMesh[out2]
reg2 = ConvexHullMesh[in2]

You can use NIntegrate over a region to get the volume (look at Volume under a List3dPlot?).

NIntegrate[1, {x, y, z} ∈ reg1] - NIntegrate[1, {x, y, z} ∈ reg1]

but for your system, you can integrate over the 2D region and multiply with $2\pi$ due to its symmetry.

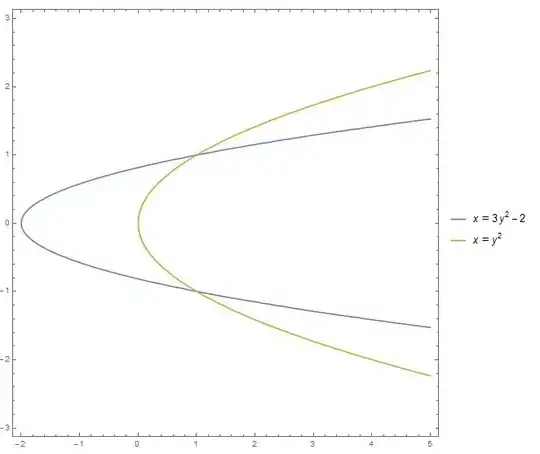
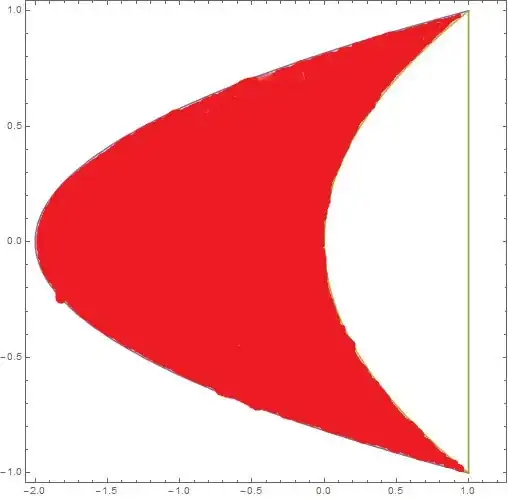
reg[x_, y_] := (x) > (3 y^2 - 2) && (x) < y^2
RegionPlot[reg[x, y], {x, -3.5, 3.5}, {y, -1.5, 1.5}, MaxRecursion -> 5]
NIntegrate[Boole[reg[x, y]], {x, -3.5, 3.5}, {y, -1.5, 1.5}]

2.66667

Answer 2

Let's solve the easier problem first:

Find the volume of the solid obtained by rotating the region bounded by the curves $x=3y^2-2$ and $x=y^2$ about the line $x=1$.

We can use Pappus's theorem for this. First, set up the region:

reg = ImplicitRegion[3 y^2 - 2 <= x <= y^2, {{x, -2, 2}, {y, -2, 2}}];

Visualize:

RegionPlot[reg]

Pappus's theorem now proceeds like this:

Area[reg] (2 π EuclideanDistance[RegionCentroid[reg], {1, 0}])
   (128 π)/15

As a plausibility check, let's compute the volume with a different method:

4 π (Integrate[Sqrt[(3 - r)/3] r, {r, 0, 3}] - Integrate[Sqrt[1 - r] r, {r, 0, 1}])
   (128 π)/15

(exercise: how did I derive this integral?)

To visualize the solid of revolution itself, we can use contourRegionPlot3D[] from this answer:

contourRegionPlot3D[(z^2 - 1)^2 <= x^2 + y^2 <= (3 z^2 - 3)^2,
                    {x, -3, 3}, {y, -3, 3}, {z, -1, 1}, ContourStyle -> Opacity[2/3]]

(exercise: how did I derive the required inequalities?)