Delete duplicates of isomerism

Question

I written some code to generate all partens of $\ \mathrm{C_2H_5O}$, but theres some isomerisms need to be deleted.

Here's the raw output after DeleteDuplicates.

(*del=DeleteDuplicates@raw*)
del={{{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"H",1}<->{"C",1},{"H",2}<->{"C",2},{"H",3}<->{"C",1},{"O",1}<->{"C",2},{"H",4}<->{"C",1}},{{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"H",1}<->{"C",1},{"H",2}<->{"C",2},{"C",1}<->{"O",1},{"H",3}<->{"C",2},{"H",4}<->{"C",1}},{{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"H",1}<->{"C",1},{"C",2}<->{"C",1},{"H",2}<->{"O",1},{"H",3}<->{"C",2},{"H",4}<->{"C",1}},{{"C",2}<->{"C",1},{"H",1}<->{"C",2},{"O",1}<->{"C",1},{"H",2}<->{"C",2},{"H",3}<->{"C",1},{"O",1}<->{"C",2},{"H",4}<->{"C",1}},{{"C",2}<->{"C",1},{"H",1}<->{"C",2},{"O",1}<->{"C",1},{"H",2}<->{"C",2},{"C",1}<->{"O",1},{"H",3}<->{"C",2},{"H",4}<->{"C",1}},{{"C",2}<->{"C",1},{"H",1}<->{"C",2},{"O",1}<->{"C",1},{"C",2}<->{"C",1},{"H",2}<->{"O",1},{"H",3}<->{"C",2},{"H",4}<->{"C",1}},{{"C",2}<->{"C",1},{"H",1}<->{"C",2},{"H",2}<->{"C",1},{"O",1}<->{"C",2},{"H",3}<->{"C",1},{"O",1}<->{"C",2},{"H",4}<->{"C",1}},{{"C",2}<->{"C",1},{"H",1}<->{"C",2},{"H",2}<->{"C",1},{"O",1}<->{"C",2},{"C",1}<->{"O",1},{"H",3}<->{"C",2},{"H",4}<->{"C",1}},{{"C",2}<->{"C",1},{"H",1}<->{"C",2},{"H",2}<->{"C",1},{"H",3}<->{"C",2},{"C",1}<->{"C",2},{"O",1}<->{"C",1},{"H",4}<->{"O",1}},{{"C",2}<->{"C",1},{"H",1}<->{"C",2},{"H",2}<->{"C",1},{"H",3}<->{"C",2},{"O",1}<->{"C",1},{"O",1}<->{"C",1},{"H",4}<->{"C",2}},{{"C",2}<->{"C",1},{"H",1}<->{"C",2},{"H",2}<->{"C",1},{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"H",3}<->{"O",1},{"H",4}<->{"C",1}},{{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"O",1}<->{"C",2},{"H",1}<->{"C",1},{"H",2}<->{"C",1},{"H",3}<->{"C",2},{"H",4}<->{"C",1}},{{"O",1}<->{"C",1},{"H",1}<->{"C",1},{"H",2}<->{"C",1},{"C",2}<->{"O",1},{"H",3}<->{"C",2},{"C",2}<->{"C",1},{"H",4}<->{"C",2}},{{"O",1}<->{"C",1},{"H",1}<->{"C",1},{"C",1}<->{"O",1},{"C",2}<->{"C",1},{"H",2}<->{"C",2},{"H",3}<->{"C",2},{"H",4}<->{"C",2}},{{"O",1}<->{"C",1},{"H",1}<->{"C",1},{"C",2}<->{"C",1},{"C",2}<->{"C",1},{"H",2}<->{"C",2},{"H",3}<->{"O",1},{"H",4}<->{"C",2}},{{"H",1}<->{"C",1},{"C",2}<->{"C",1},{"H",2}<->{"C",2},{"H",3}<->{"C",2},{"C",1}<->{"C",2},{"O",1}<->{"C",1},{"H",4}<->{"O",1}},{{"H",1}<->{"C",1},{"C",2}<->{"C",1},{"H",2}<->{"C",2},{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"H",3}<->{"O",1},{"H",4}<->{"C",1}},{{"H",1}<->{"C",1},{"H",2}<->{"C",1},{"C",2}<->{"C",1},{"H",3}<->{"C",2},{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"H",4}<->{"O",1}},{{"H",1}<->{"C",1},{"H",2}<->{"C",1},{"C",2}<->{"C",1},{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"H",3}<->{"O",1},{"H",4}<->{"C",2}},{{"H",1}<->{"C",1},{"H",2}<->{"C",1},{"H",3}<->{"C",1},{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"C",2}<->{"O",1},{"H",4}<->{"C",2}}}
show=Graph[#, GraphLayout->"SpringEmbedding",
  VertexStyle->{{"C",_}->Lighter[Black],{"O",_}->Lighter[Red],{"H",_}->LightBlue,{"N",_}-> Lighter[Blue]},
  EdgeStyle-> Darker@Green,VertexSize->{{"C",_}->0.7,{"O",_}->0.5,{"H",_}->0.4,{"N",_}->0.6}, 
  ImageSize->{210,200}]&;
Multicolumn@DeleteDuplicates[show/@del]

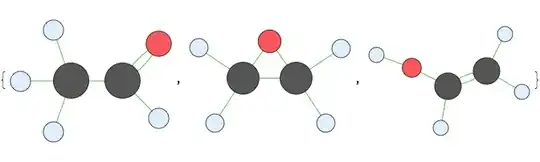
The last one is the same as blue ones (not the red one) in 2D. And IsomorphicGraphQ would delete all but first one.

How can I delete these duplicates one?

Just consider planar isomerism, and I also glad to see if anyone solved the stereo isomerism.

---

Edit:

I don't know why you can't reproduce this.

I restarted my Kernels and got the same results.

$Version
show=Graph[#,GraphLayout->"SpringEmbedding",
    VertexStyle->{{"C",_}->Lighter[Black],{"O",_}->Lighter[Red],{"H",_}->LightBlue,{"N",_}->Lighter[Blue]},
    EdgeStyle->Darker@Green,VertexSize->{{"C",_}->0.7,{"O",_}->0.5,{"H",_}->0.4,{"N",_}->0.6},
    ImageSize->{210,200}]&;
del={
    {{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"H",1}<->{"C",1},{"H",2}<->{"C",2},{"H",3}<->{"C",1},{"O",1}<->{"C",2},{"H",4}<->{"C",1}},
    {{"C",2}<->{"C",1},{"H",1}<->{"C",2},{"O",1}<->{"C",1},{"H",2}<->{"C",2},{"C",1}<->{"O",1},{"H",3}<->{"C",2},{"H",4}<->{"C",1}},
    {{"C",2}<->{"C",1},{"O",1}<->{"C",2},{"H",1}<->{"C",1},{"H",2}<->{"C",2},{"C",1}<->{"O",1},{"H",3}<->{"C",2},{"H",4}<->{"C",1}}
};
Quiet@DeleteDuplicatesBy[show/@del,CanonicalGraph]
DeleteDuplicatesBy[show/@del,IsomorphicGraphQ]

These are {1,2,5} of last del.

If still have problems I may need to reinstall my Mathematica :).

Answer 1

It is true that the built-in function IsomorphicGraphQ does not consider vertex color (atom types) or multi-edges (double and triple bonds). It would be nice if there were an IsomorphicMoleculeQ function, but we can make do with an external library.

The CDK java library is easy to use, and well-documented. JLink makes it easy to use a java library without writing any java code.

Here is an example of how to use it for deleting duplicates based on chemical isomorphism. In the code below, I first convert a bond list into an AtomContainer, then use the UniversalIsomorphismTester class to compare the molecules.

First download the latest release of CDK. Change the file path below to the downloaded location for your system.

<< JLink`

AddToClassPath["~/Downloads/cdk-2.1.jar"];
(* necessary to load this enum class separately *)
LoadJavaClass["org.openscience.cdk.interfaces.IBond$Order"];

$bondPattern = (UndirectedEdge | TwoWayRule)[{_String, _Integer}, {_String, _Integer}];

bondListToAtomContainer[bondList : {$bondPattern ..}] := 
  bondListToAtomContainer[bondList] =
   Block[{bonds, atomList, mol},
    (* convert each bond into a list of {{id1, id2}, bondorder} *)
    (* and make a list of atomic symbols for the atoms *)
    bonds = List @@@ bondList;
    bonds = Sort /@ bonds;
    atomList = Flatten[bonds, 1] // Union;
    atomList = Thread[atomList -> Range[0, Length@atomList - 1]];
    bonds = bonds /. atomList;
    bonds = 
     Tally[bonds] /. {{a1_, a2_}, n_} :> {{a1, a2}, 
        n /. {1 -> IBond$Order`SINGLE, 2 -> IBond$Order`DOUBLE}};
    atomList = atomList[[All, 1, 1]];
    (* now create an empty molecule, then add the atoms and bonds *)
    mol = JavaNew["org.openscience.cdk.AtomContainer"];
    Do[
     mol@addAtom[JavaNew["org.openscience.cdk.Atom", atom]],
     {atom, atomList}];
    Do[ 
     mol@addBond[ bond[[1, 1]], bond[[1, 2]], bond[[2]]],
     {bond, bonds}
     ];
    (* return the molecule *)
    mol];
(* now instantiate a UniversalIsomorphismTester *)
isomorphismTester := 
  isomorphismTester = 
   JavaNew["org.openscience.cdk.isomorphism.UniversalIsomorphismTester"];

(* Finally a function to test if two molecules, 
   represented by bond lists, are isomorphic *)
isomorphicMoleculeQ[bondList1 : {$bondPattern ..}, 
  bondList2 : {$bondPattern ..}] :=
 isomorphismTester@isIsomorph[
   bondListToAtomContainer@bondList1, 
   bondListToAtomContainer@bondList2]

If I define del and show as the list in the OP, I can use the 2-argument form of DeleteDuplicates,

DeleteDuplicates[del,
 isomorphicMoleculeQ
 ]
(* {{{"C", 2} <-> {"C", 1}, {"O", 1} <-> {"C", 2}, {"H", 
    1} <-> {"C", 1}, {"H", 2} <-> {"C", 2}, {"H", 3} <-> {"C", 
    1}, {"O", 1} <-> {"C", 2}, {"H", 4} <-> {"C", 1}}, {{"C", 
    2} <-> {"C", 1}, {"O", 1} <-> {"C", 2}, {"H", 1} <-> {"C", 
    1}, {"H", 2} <-> {"C", 2}, {"C", 1} <-> {"O", 1}, {"H", 
    3} <-> {"C", 2}, {"H", 4} <-> {"C", 1}}, {{"C", 2} <-> {"C", 
    1}, {"O", 1} <-> {"C", 2}, {"H", 1} <-> {"C", 1}, {"C", 
    2} <-> {"C", 1}, {"H", 2} <-> {"O", 1}, {"H", 3} <-> {"C", 
    2}, {"H", 4} <-> {"C", 1}}} *)

show /@ %

A more efficient way to do this might be to convert each molecule into a canonical SMILES string, which the CDK can do quite well.

Answer 2

The answer below requires IGraph/M 0.3.96 or later. If you have an earlier version, please upgrade.

If we only consider the connectivity of the atoms, not their spatial arrangements, we can remove duplicates based on graph isomorphism. This can be done in one of two ways:

DeleteDuplicatesBy[graphs, CanonicalGraph]

or

DeleteDuplicates[graphs, IsomorphicGraphQ]

The first solution is preferable because it has linear complexity in the number of graphs/molecules, while the second is quadratic.

Unfortunately, in Mathematica 11.2 for Windows most of the isomorphism functionality is broken. (Earlier versions and Linux/Mac are not affected.)

There is also the major problem that the builtin isomorphism functionality does not currently support either multigraphs (multiple bonds between the same atoms) or vertex colouring (i.e. restricting mappings to between identical types of atoms).

---

IGraph/M provides some, but not all of this functionality. Out of the box, it supports either isomorphism with vertex colouring (i.e. distinguishing atom types) or multigraph isomorphism, but not both simultaneously. If you need both, you can map edge multiplicity to edge colours, and use IGVF2IsomorphicQ.

However, it seems to me that for this application, edge multiplicity can be ignored. Let us thus focus only on vertex colours now.

IGraph/M requires vertex colours to be integers. Let us start by transforming the atom names to integers, and storing the result in the "Color" vertex property. The following vertex map operator does this:

atomToNumber = <|"H" -> 1, "C" -> 6, "O" -> 8|>;

IGVertexMap[atomToNumber @* First, "Color" -> VertexList]

Before applying it, we need to get rid of multi-edges. We can use SimpleGraph for that. It needs to be applied before the above function because, unfortunately, it discards vertex properties.

Finally, we will use IGBlissCanonicalGraph instead of CanonicalGraph. It supports vertex colouring. We need to tell it which property contains the colours.

Putting all of it together,

graphs = show /@ del

atomToNumber = <|"H" -> 1, "C" -> 6, "O" -> 8|>;

DeleteDuplicatesBy[
 graphs,
 IGBlissCanonicalGraph[{#, "VertexColors" -> "Color"}] & @*
  IGVertexMap[atomToNumber @* First, "Color" -> VertexList] @*
  SimpleGraph
]

A slightly different way to accomplish the same is to forget about vertex properties and specify the colours as a plain list.

DeleteDuplicatesBy[
 graphs,
 IGBlissCanonicalGraph[{SimpleGraph[#], "VertexColors" -> atomToNumber /@ First /@ VertexList[#]}] &
]