1

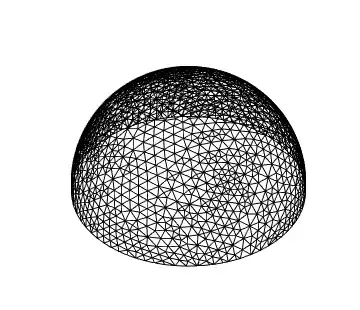
While trying to create a surface mesh of a hemisphere

<< NDSolve`FEM`
halfsphere = ImplicitRegion[x^2 + y^2 + z^2 == 1 && z >= 0, {x, y, z}]
reg = DiscretizeRegion[halfsphere]

I get the expected plot enter image description here,

but some questions remain:

  • How could I show the mesh of reg?
  • Why isn't it possible to create an elementmesh from reg?
    ToElementMesh[reg]
    (* ToElementMesh::femtemnm: A mesh could not be generated. *)
  • How could I extract the boundary (equator)?

Thanks!

user21
  • 39,710
  • 8
  • 110
  • 167
Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55

3 Answers3

3

For first question:

MeshRegion[reg, MeshCellStyle -> {1 -> Black}]

or

MeshRegion[reg, PlotTheme -> "Default"]

or

MeshRegion[reg, PlotTheme -> "Lines"]

To find the equator you could use FindMeshDefects:

boundary = FindMeshDefects[reg, "HoleEdges", "Cell"]["HoleEdges"]

{{Line[{392, 460, 464, 911, 978, 1029, 1086, 1137, 1184, 1235, 1286, 1339, 1390, 1457, 1512, 1537, 569, 570, 637, 638, 701, 702, 769, 765, 766, 817, 813, 856, 853, 849, 844, 839, 834, 829, 824, 820, 778, 773, 717, 710, 705, 647, 641, 579, 573, 476, 475, 1516, 1463, 1393, 1343, 1291, 1241, 1190, 1143, 1092, 1035, 983, 917, 857, 401, 400, 337, 264, 263, 196, 195, 121, 120, 129, 63, 62, 1, 7, 12, 18, 24, 30, 36, 42, 47, 51, 54, 110, 114, 180, 186, 189, 254, 257, 326, 329, 392}]}}

HighlightMesh[reg, boundary]
halmir
  • 15,082
  • 37
  • 53
2

Ulrich, please have a look at the documentation. For example, ToBoundaryMesh, ToElementMesh and the Element Mesh Generation tutorial have plenty of information.

<< NDSolve`FEM`
halfsphere = ImplicitRegion[x^2 + y^2 + z^2 == 1 && z >= 0, {x, y, z}];
reg = ToBoundaryMesh[halfsphere];
reg["Wireframe"]

enter image description here

For the equator you could look at ElementMesh and the mentioned "BoundaryConnectivity" or "VertexBoundaryConnectivity"

If you want to extract the coords use something like:

Cases[reg[
  "Coordinates"], {_?NumericQ, _?NumericQ, _?(Abs[#] <= 10^-3. &)}]
user21
  • 39,710
  • 8
  • 110
  • 167
  • Thank you for the helpful answer. If I consider a little more complex problem, which I tried to prepare with my question: A closed curve, on the sphere cuts the sphere in two parts. How would I mesh such a surface? – Ulrich Neumann Jan 06 '18 at 10:48
1

Inspecting the documentation:

reg = DiscretizeRegion[halfsphere, 
MeshCellHighlight -> {{1, All} -> Black}, MaxCellMeasure -> .005]

enter image description here

You can play with MaxCellMeasure value.

Now, you have a 2D region, so you have to use ToBoundaryMesh:

ToBoundaryMesh[halfsphere]["Wireframe"]

enter image description here

And finally, I am assuming you need the coordinates of the resulting mesh for the equator:

Cases[ToBoundaryMesh[halfsphere, {{-1, 1}, {-1, 1}, {0, 1}}]["Wireframe"][[1, 2, 1]]
, {__, __, 0.}]
José Antonio Díaz Navas
  • 6,103
  • 1
  • 20
  • 30